Physiological Monitoring
Notes for lectures on Cardiovascular Measurements
by K.H. Parker
Lecture 1: Basic Physical Principles
"You have to know what you are
measuring before you can measure it"
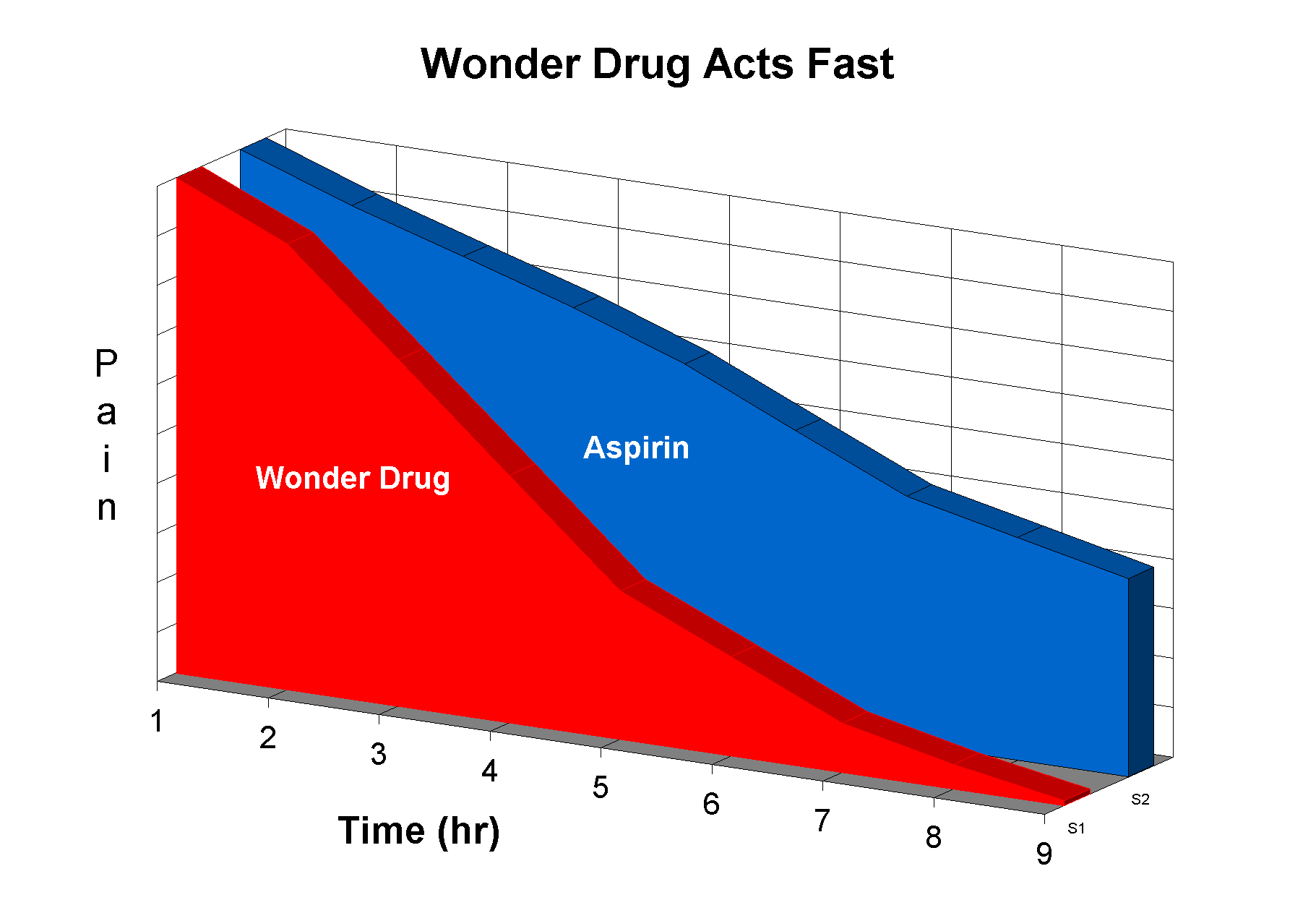
What is wrong with this plot?
Basic concepts
1. Mass dimension [M], SI unit (kg)
- A basic property of matter.
- It is a scalar.
- It is virtual impossible to measure directly (see below).
- We all have a 'sense' of time, but it is very difficult to define.
- See A Brief History of Time by Stephen Hawking for more more information.
- Time is relative; i.e. it must be expressed relative to a some reference time.
- It is a scalar.
in Islamic societies the year is 1420 AH
computesr measure time from 1 Jan 1970
3. Position dimension [L], SI unit (m)
- Position is relative, it can only be measured relative to some frame of reference
- It is a vector; i.e. it has both magnitude and direction.
In mechanics, these three properties are considered to be the basic
units, all other mechanical variables can be expressed in terms of them.
4. Velocity
If position is a function of time, X(t), we can define the rate of
change of position by considering the ratio of the change of position to
the change of time,
Note that there is an intimate connection between mechanics
and calculus which is not surprising because calculus was invented by Newton
and Liebnitz to assist their study of mechanics. Until the start of the last
century, nearly all advances in applied mathematics were motivated by problems
in mechanics.
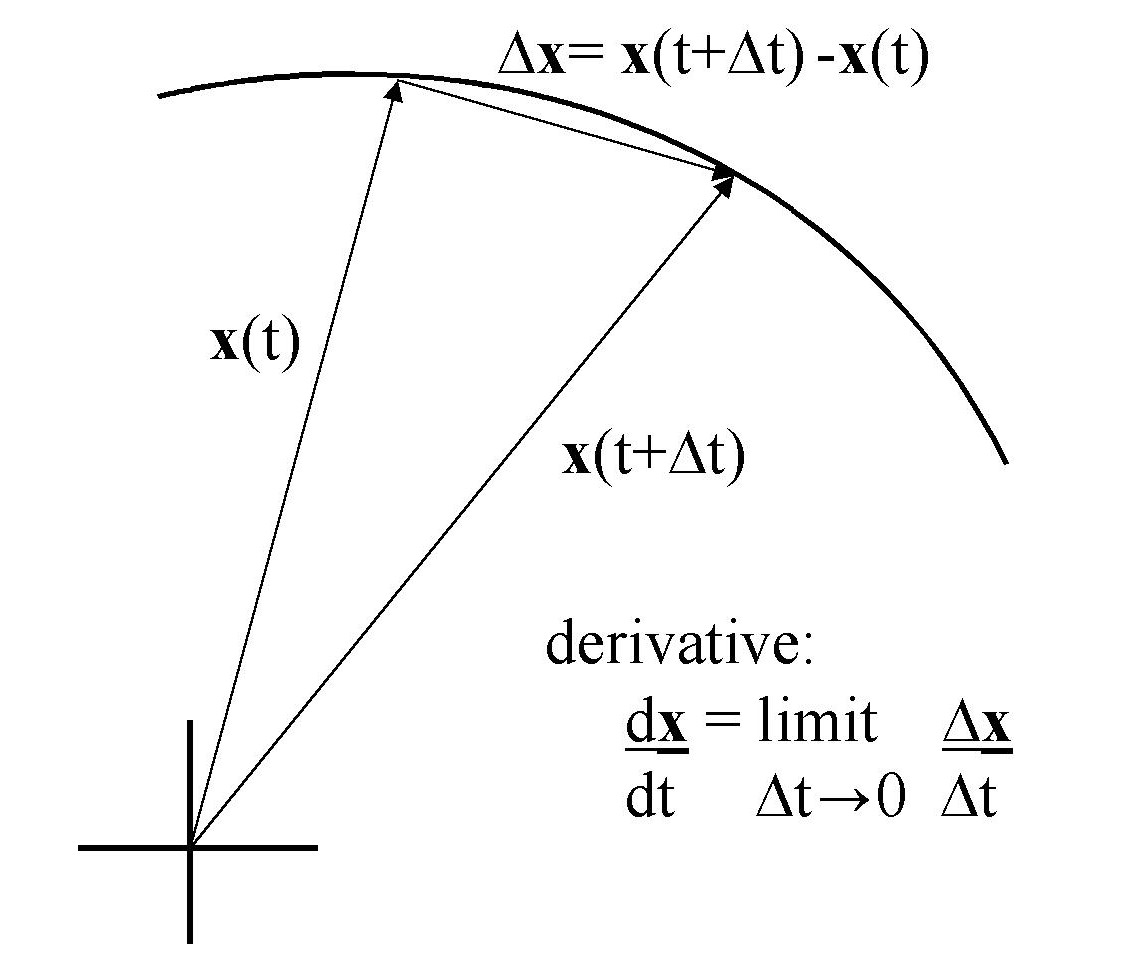
- From the definition of velocity we can see that velocity is a vector (a vector divided by a scalar is a vector).
- The dimension of velocity also follows from the dimensional integrity
of the defining equation; i.e. dimension [L][T]-1, SI units
(m/s).
5. Acceleration
Velocity is a function of time, V(t), and so we can similarly define the rate of change of velocity
The example to the left shows what happens when an object is tossed into
the air when the force of gravity is constant. Position is the height of
the object which starts at ground level (zero height), reaches a peak height
and then falls back to ground. Initially the velocity is positive, the object
is initially moving upward. The velocity decreases linearly until zero velocity
is attained at the time that the object reaches its maximum height. Then
the velocity gets more and more negative until it strikes the ground with
speed (magnitude of velocity) as it left at time zero.
The example to the right follows a more complicated path. Note that zeros in velocity correspond to the local maxima and minima in position. Similarly, maxima and minima in the velocity correspond to points of zero acceleration which correspond to points of inflection in the position. Velocity is the slope of position. Acceleration is the slope of the velocity.
6. Force
In addition to moving around in space, bodies interact with each other. These mechanical interactions are called forces. There are many types of forces; muscular forces (pulling and pushing), gravitational, hydrodynamic, magnetic... One of Newton's great contributions to human understanding was his concept of a general force, i.e.that all of these different forces were different manifestations of the same thing.
which you probably know as 'F=ma'. This, however, is a special case of what Newton actually stated (see below)
Fluid Mechanics
Velocity is a function of time, V(t), and so we can similarly define the rate of change of velocity
A(t) = dV = d d
X = d2X
dt dt dt dt2
dt dt dt dt2
- Acceleration is a vector.
- The dimensions of acceleration are [L][T]-2, SI units (m/s
2)
The example to the right follows a more complicated path. Note that zeros in velocity correspond to the local maxima and minima in position. Similarly, maxima and minima in the velocity correspond to points of zero acceleration which correspond to points of inflection in the position. Velocity is the slope of position. Acceleration is the slope of the velocity.
6. Force
In addition to moving around in space, bodies interact with each other. These mechanical interactions are called forces. There are many types of forces; muscular forces (pulling and pushing), gravitational, hydrodynamic, magnetic... One of Newton's great contributions to human understanding was his concept of a general force, i.e.that all of these different forces were different manifestations of the same thing.
- Force is a vector, it has both magnitude and direction.
which you probably know as 'F=ma'. This, however, is a special case of what Newton actually stated (see below)
F = d (MV)
dt
where F is the net force (the sum of all of the forces acting on a body) and MV is known as the momentum.
dt
where F is the net force (the sum of all of the forces acting on a body) and MV is known as the momentum.
In the special case when the mass of the body is constant
in time (the usual case in biomechanics)
F = d (MV) = M dV
= MA
dt dt
dt dt
- From Newton's Second Law, we see that the dimensions of force are [M][L][T] -2, in SI units (kg m/s2) this is also defined as (N)
Newton's second law is the basis of virtually all of mechanics.
Since Einstein's theory of relativity, we know that this law breaks down
when velocities approach the speed of light. Apart from this, Newton's second
law has been very well tested and must be considered as much of a 'law' as
there is in science. (Remember that scientific hypotheses can only be disproved,
not proved.)
7. Work and Energy
7. Work and Energy
Because it is more difficult to work with vectors, it is
convenient to define scalars that characterise the dynamics of a body. Work
and energy are two very useful scalar properties.
Work: Work is defined as the integral of the scalar
product of force and distance moved
W = Integral(F · dx)
-
The dimensions of work are [M][L]2[T]-2; in SI units (kg m2/s2) defined as (W).
Energy: There are several types of energy. Two examples are:
- Kinetic energy:
KE = ½ MV2
- Potential energy due to gravity:
PE = Mgh
where g is the acceleration due to gravity and h is the height.
-
The dimensions of energy are the same as work, [M][L]2[T]-2
-
When there is no dissipation, the change in total energy in a system is equal to the work done on it. If no external work is done on the system, the total energy is constant.
-
Energy is also important when we consider interactions which are not simply mechanical. In the body, for example, we generally have to consider chemical energy (metabolism) and thermal energy (heat).
Fluid Mechanics