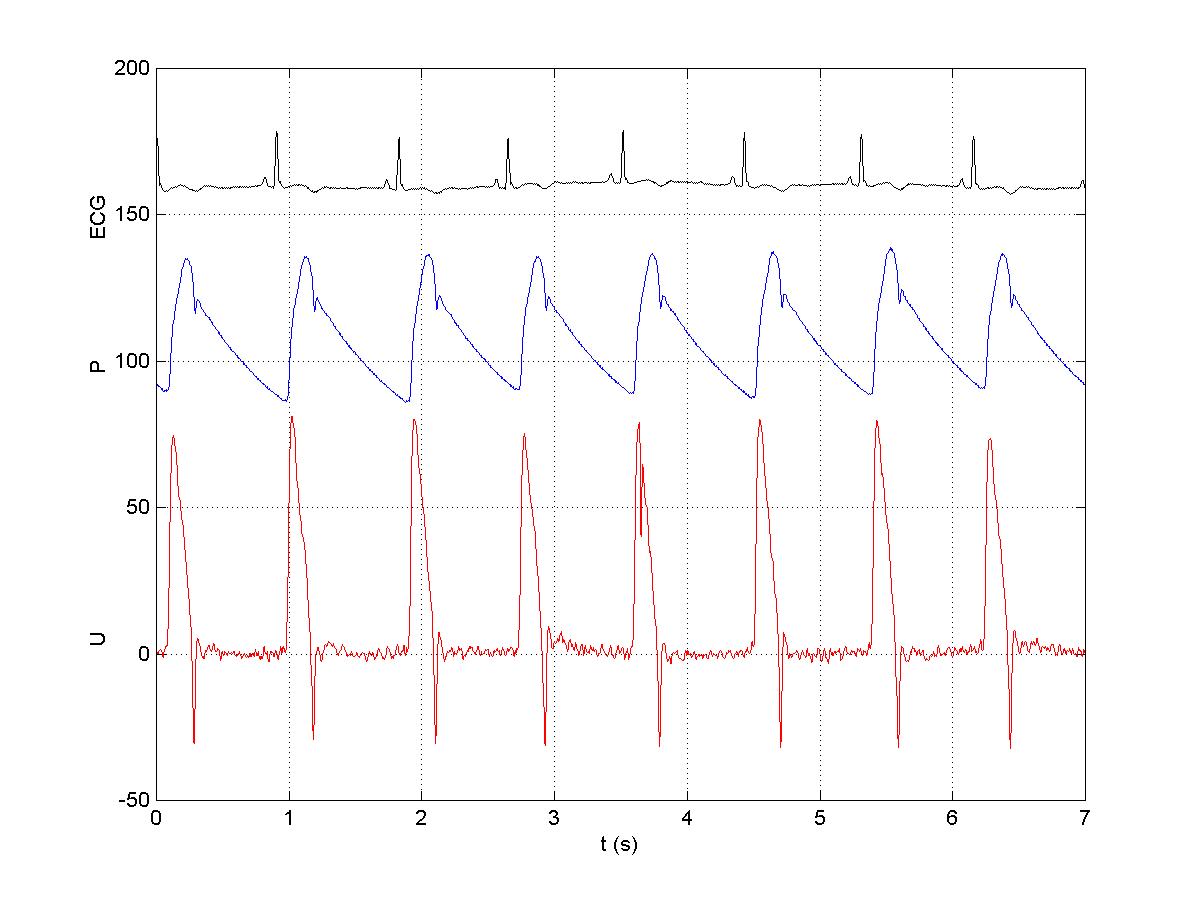
The figure shows the ECG (for reference), the pressure (P) in mmHg and the velocity (U) in cm/s in the ascending aorta. These data were measured invasively using a catheter.

One of the prominent features of arterial flow is that the pressure and velocity produced by the contraction of the left ventricle (LV) produce a wave which propagates throughout the arterial system, the pulse wave. These waves were first analysed scientifically by Thomas Young in his Croonian Lecture to the Royal Society in 1808.

Note that the flow is very pulsatile, increasing rapidly, reaching a peak, decelerating until the reversal of flow through the aortic valve closes the valves at the end of systole. There is no  velocity during most of diastole. This is not true of flow in the carotid artery (and the uterine artery in pregnancy) where the flow is still pulsatile but there is substantial forward flow during the whole of diastole. Why do you think this is?

The 'stroke' volume ejected by the LV (approximately 50 ml) is slightly less than the volume of the ascending aorta. Therefore, the blood reaching the microcirculation is several heart beats 'away' from the LV.

Note that the pattern of flow in the coronary arteries is very different. Because the contraction of the myocardium occludes the vessels within it, flow during systole is either zero or greatly reduced. When the myocardium relaxes, blood can once again flow through the coronary microcirculation and so flow in the coronary arteries is highest during diastole. It has been argued that the need to perfuse the heart during diastole is the reason that the mean blood pressure in the systemic circulation is high. It has to drive flow through the coronary circulation during diastole.

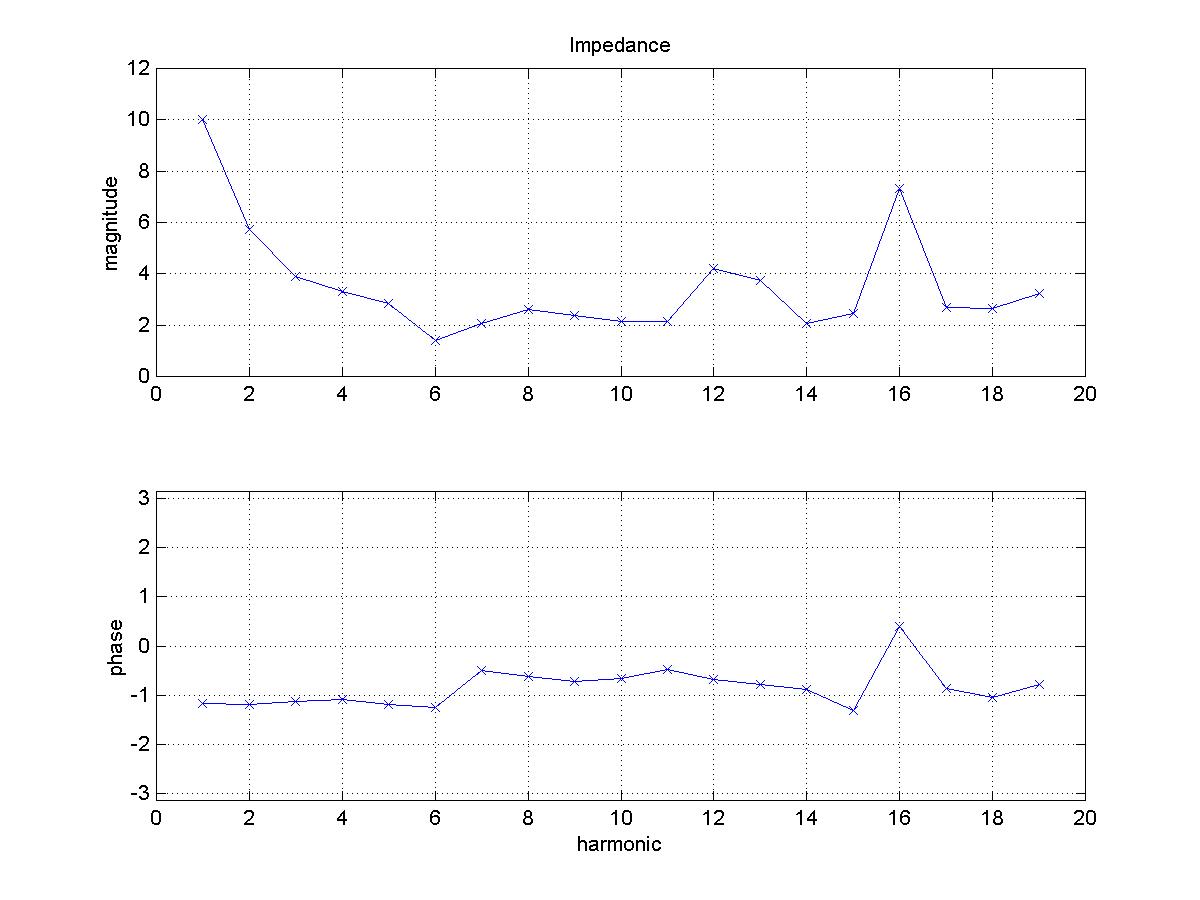
Impedance Analysis

The standard way of analysing pressure and flow in the arteries is a Fourier transform based method generally known as impedance analysis in reference to the analogous analysis of electrical circuits.

Refer to:

Nichols and O'Rourke, MacDonald's Blood Flow in the Arteries (4th ed.).

Milnor, Hemodynamics.

In this method, the pressure, P(t), and velocity, U(t) (or, alternatively, the volume flow rate), are expressed as the linear superposition of sinusoidal waveforms using the Fourier transform

P(w) = F{P(t)}

 U(w) = F{U(t)}

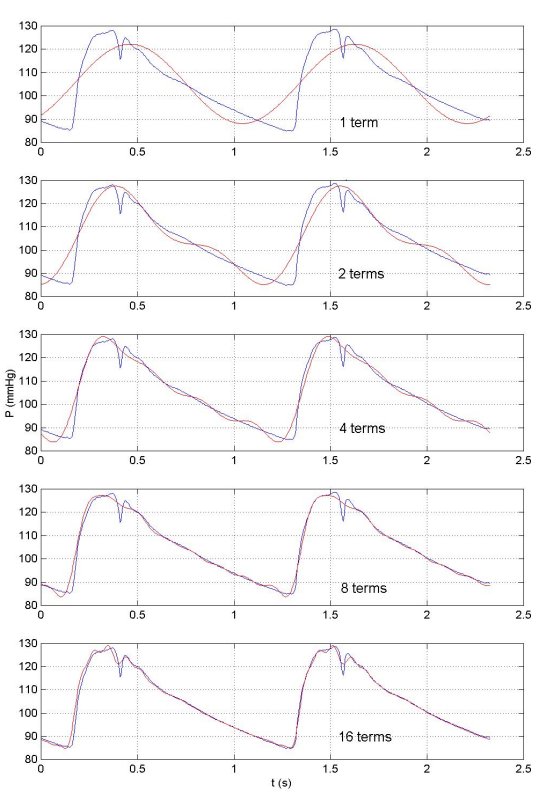
Surprisingly few harmonics are necessary to build  up a very good approximation to the experiementally measured waveforms. This is shown here where the original waveform (in blue) is compared to the first harmonic wave (in red), the sum of the first and second harmonics, the sum of the first four harmonics, eight harmonics and finally sixteen harmonics. We see that sixteen harmonics are sufficient to reproduce most of the detail of the measured waveform.

Because the Fourier transform is complete, summing all of the harmonics will give the initial waveform exactly, noise and all.

By analogy to Ohms law, relating voltage and current in electrical circuits, it is assumed that the pressure and velocity for each harmonic are related

P(w) = U(w) Z(w)

where Z(w) is called the impedance. Because P(w) and U(w) are complex numbers (they have a real and imaginary part), Z(w) is also complex. It is usually represented by the polar form, i.e. its magnitude |Z| and phase f, where

Z(w) = |Z| e^if

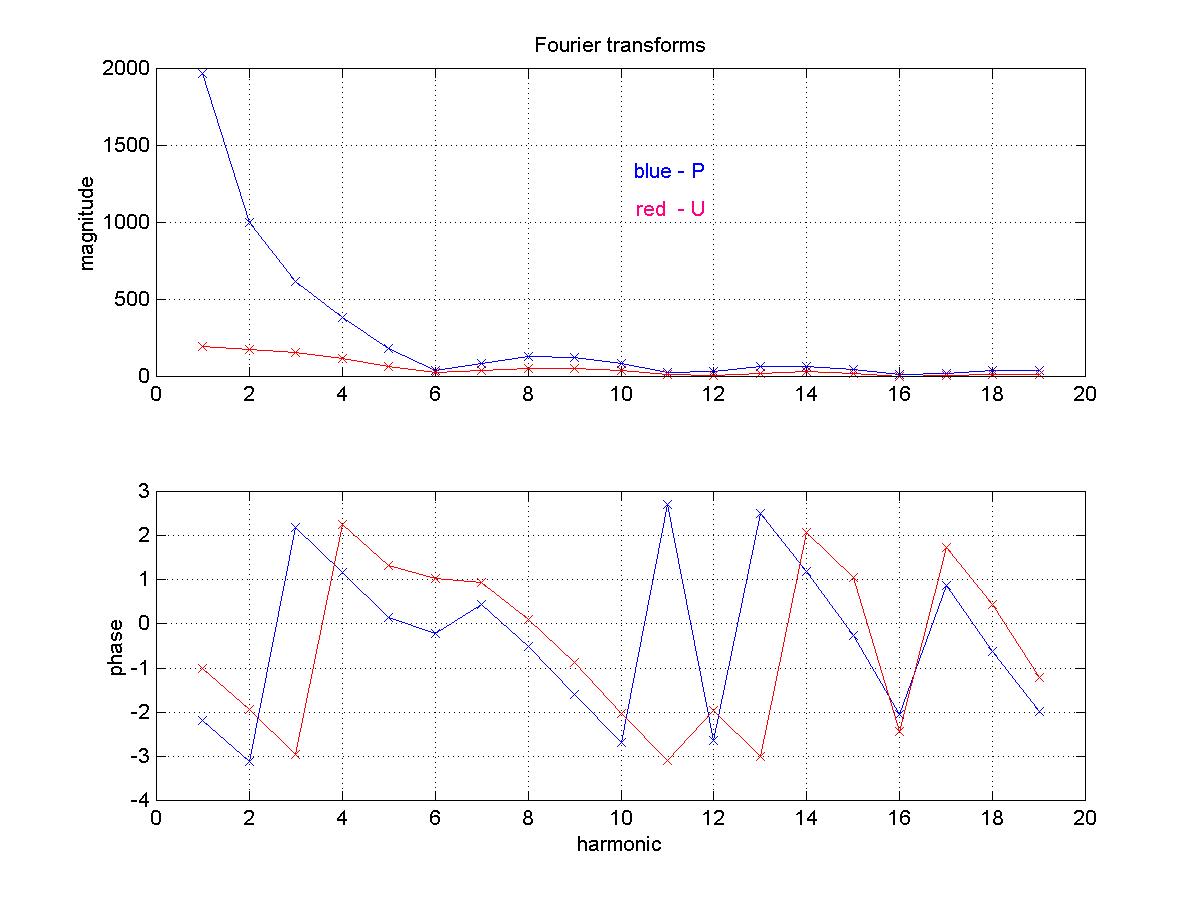
For the data shown previously, the second beat in the figure showing P and U above,

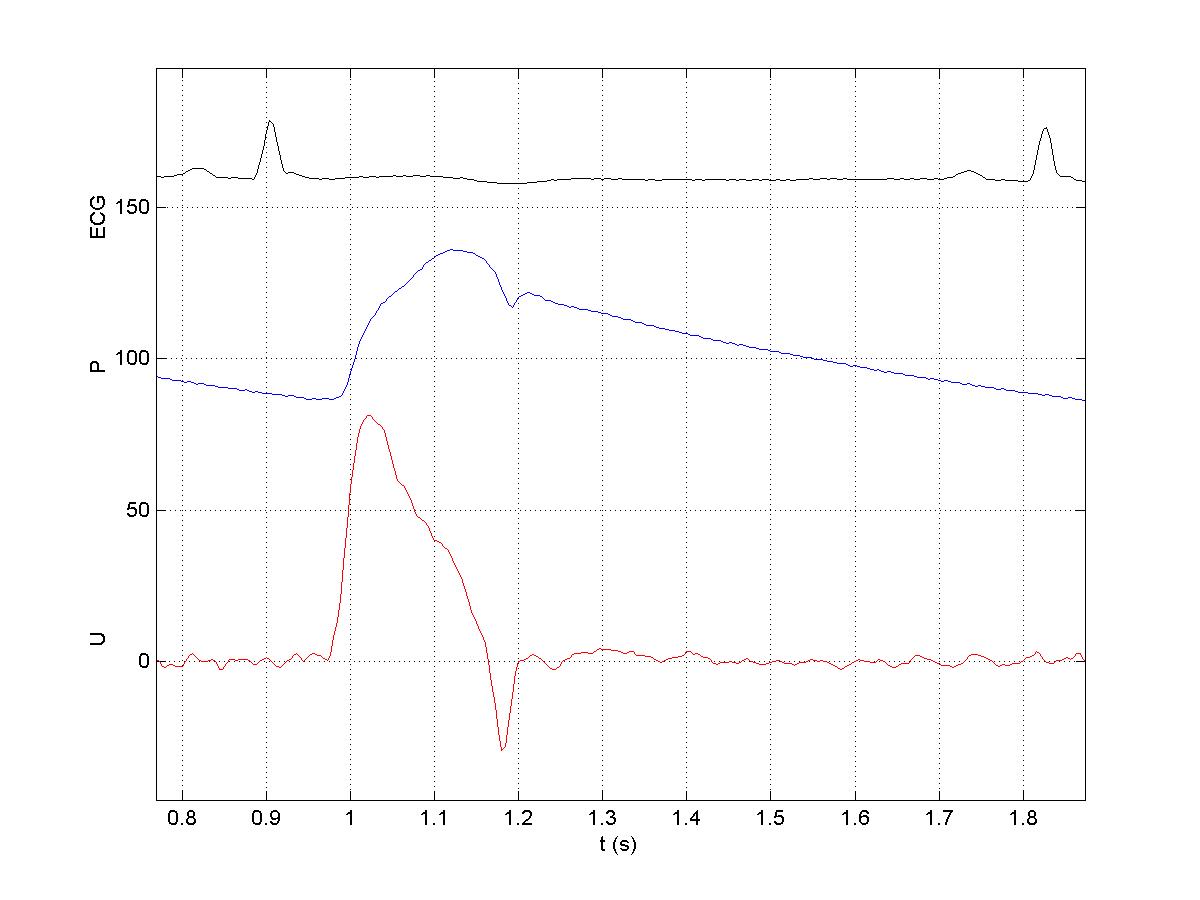
the P(w) and U(w), magnitude and phase, are

The impedance, magnitude and phase, calculated from these data is