Wave intensity analysis uses an alternative view of arterial waves from most, if not all, textbooks on haemodynamics. To justify this approach, it is useful to think about waves generally. Hence, this homily on 'waves'.
There are many definitions of 'wave' and many sites on the web that give definitions and examples of different waves. Interestingly, most articles defining waves start by saying how difficult it is to find a simple, universal definition of 'wave'. I would agree with them.
There is general agreement that waves are important and that waves are all around us; sound waves, light waves, radio waves, water waves, etc. etc. It is difficult, however, to find a succinct definition of 'wave' that embraces all sorts of physical waves. The definition that we will use is perhaps the simplest:
Waves: disturbances that propagate in space and time.
The physics underlying this propagation invariably involves some exchange of energy from one form to another as the wave passes. A sound wave, for example, involves the transfer of the kinetic energy of the fluid particles into the potential energy involving changes in pressure (remember that pressure has the units energy/volume). Similarly, surface waves on water involve the transfer of energy between potential energy due to gravity (changes in the height of the water) and the kinetic energy of the water (the velocity of the water particles as they move up and down). Electromagnetic waves, which include light waves, involve the exchange between electric and magnetic energy which, unlike most other waves, does not require a substrate and they can therefore propagate through the vacuum of space.
Most of the waves that we experience are periodic in nature: sound, light, and surface waves on water. Fourier analysis is a convenient way to analyse these waves. The periodic wave is thought of as the superposition of sinusoidal wave trains at a fundamental frequency and all of its harmonics. It is possible to describe any periodic wave by the appropriate choice of amplitude and phase of these elemental wave trains. In many cases, the speed of propagation of these sinusoidal wave trains depends upon their frequency.
The superposition of wave trains with different frequencies and wave speeds can have many interesting results, generally termed dispersion. The combination of wave trains can have patterns of peaks and troughs, generally described by their envelope, which move at a velocity different from the wave speeds of the elemental wave trains; this is referred to as the group velocity. The group velocity can be greater or less than the phase velocity of the elemental wave trains; it can even be negative! (an example of a negative group velocity by Greg Egan.).
There are, however, many examples of waves that are not periodic, shock waves in gases, tsunamis and bores are common examples (everything you wanted to know about the Severn Bore - and more.) (Is this the first natural phenomenon with its own web site?). The first 'solitary' wave that was described scientifically was a water wave observed on the Union Canal near Edinburgh by John Scott Russell. When a boat stopped suddenly, he observed that the bow wave continued to propagate forward in the form of a 'well-defined heap of water' which continued along the canal without changing its form or its velocity. He followed the wave on horseback at a speed of 8 to 9 miles and hour for one or two miles before he lost it. His report of the wave to the 14th meeting of the British Association for the Advancement of Science in York in 1845 was largely forgotten until the emergence of non-linear dynamics in the 1960's when these solitary waves were dubbed solitons. Soliton solutions of the Korteweg-de vries equation which was derived to model shallow water waves were described by Zabusky and Kruskal in 1965 and an analytical solution was found by Gardner, Greene, Kruskal and Miura in 1967. These solutions propagate unchanged and show interesting behaviour when they interact with one another (non-linear interaction between solitons).
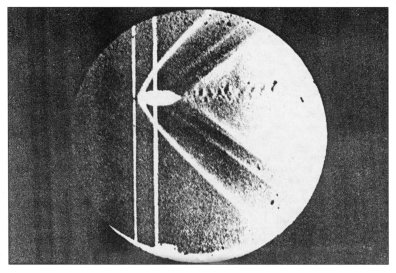
Shock waves develop when an object moves through a gas with a velocity greater than the speed of sound in the gas. This was first observed by Ernst Mach in the last half of the 19th century. This photograph published in 1877 shows the bow shock and trailing shock produced by a bullet moving at a supersonic speed from right to left. The shocks are made visible by an optical method, called a shadowgraph, which he invented. The ratio of velocity to wave speed has been named the 'Mach number' in his honour.
With the advent of supersonic flight during the Second World War, compressible gas dynamics became an area of intense research and it is now a mature, well-developed field of aeronautics.
A plane moving faster than the speed of sound creates shock waves that form a cone around the plane, just as a boat moving faster than the speed at which water waves propagate creates a V-shaped bow wave. This photograph of a fighter plane 'emerging' from a cloud is a striking manifestation of this this phenomenon. The plane is flying at supersonic speed at low altitude over an ocean in humid conditions. The compression caused by the conical shock waves around the plane causes the water vapour to condense forming the cloud over the rear of the plane, thereby making the effect of the shock waves visible. Rather than the plane emerging from the cloud, the cloud is moving with the plane. (This is undoubtedly far from the cloud that Wordsworth evokes in 'I Wandered Lonely as a Cloud', but beautiful in its own way.)
The ideas and methods developed in gas dynamics are now common in many areas of science; from cosmology and astronomy to non-linear optics and detonations. Wave intensity analysis is the application of these ideas to waves in the arteries.