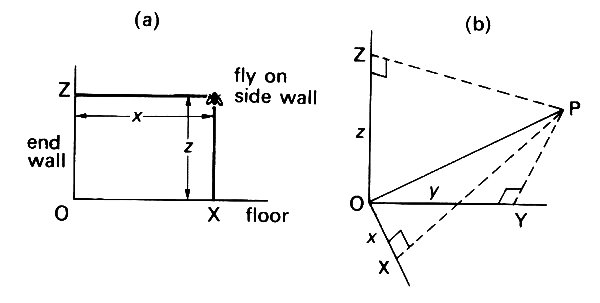
In order to describe the motion of a particle we must be able to describe accurately its position in space, which changes as the particle moves. To do this we suppose three straight lines to be drawn and fixed in space, all passing through a given point 0, and each one perpendicular to the other two. The lines of intersection of two walls and the floor of a room are examples, with 0 in the corner of the room. If a fly were walking on the wall of the room (Fig. 2.1 (a)),

Fig. 2.1. (a) The position of a fly on the side wall of a room, specified by its distance x from the end wall and its distance z from the floor; x and z are its coordinates relative the the axes formed by the lines OX, OZ. (b) The position of a point P in three dimensions (a fly flying in a room) can be specified by its distances (x, y, z) from three mutually perpendicular planes (two walls and the floor). The coordinates of P are (x, y,z). The corner of the room 0 is the origin of coordinates.
we could specify its position at any instant by recording its distance (say z) from the floor and its distance (say x) from a perpendicular wall. Similarly, if the fly were flying in the room, its position could be specified by recording its perpendicular distances from the three mutually perpendicular planes (the floor and two walls). So with any point P whose position we wish to specify. Suppose that lines are drawn through P which intersect the three original lines at right angles at the points X, Y, Z (Fig. 2.1 (b)). The three lengths OX (say x), OY(y), and OZ(z) then uniquely specify the position of P. These lengths are called the coordinates of P with respect to the three axes through 0. The lines OX, OY, and OZ are usually called the x-axis, y-axis and z-axis respectively. The total distance of P from 0 can be shown from Pythagoras's theorem to be equal to (x2+y2+z2)1/2; this quantity is independent of the directions of the axes.
It is essential to remember two things implicit in this description. First, although the choice of the point 0 and the three axes is arbitrary, once it has been made it must be adhered to consistently. For instance, it would be hopeless to try to discuss the interaction between two particles if their positions were specified in relation to different corners of the room. We usually choose axes in the most convenient way—for example, if a particle is moving about on a flat plane (the fly on the wall), it is sensible to take one of the axes (say OY) perpendicular to that plane, so that y always remains constant and only two lengths, x and z, need be specified. Secondly, the units of length by which x, y, and z are measured must be specified explicitly, and always used consistently. A length is not just a number, it is a quantity with dimension, and units are required to measure it. In this book, we shall usually use metres (m) or centimetres (1 cm = 10-2 m) or micrometres (1 mm = 10-6 m); the whole question of units will be fully discussed later (Chapter 3).
Another quantity of importance in describing the motion of a particle is its velocity, or the rate at which its position changes. Consider a particle moving along a straight line, OX (Fig. 2.2 (a)),
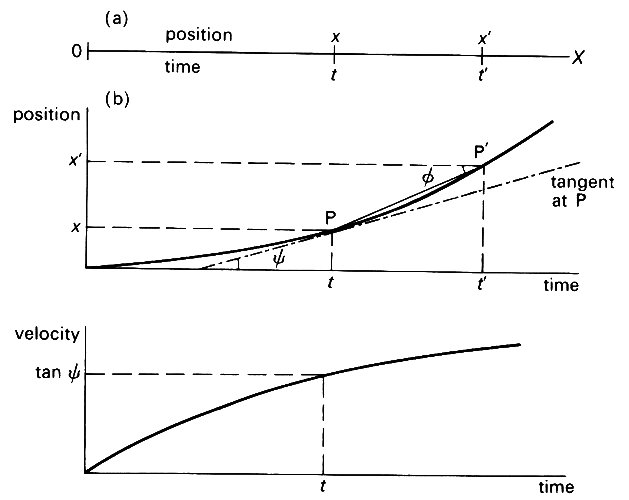
Fig. 2.2. (a) A particle moving along a line OX is at distance x from a fixed point 0 at time t, and at distance x' at a later time ('. The quantity (x'-x)/(t'-t) is the average velocity of the particle during the time interval from t to t'. As this interval is made shorter, so that t' - t tends to zero, x' - x also becomes shorter, but the average velocity tends to a well-defined limit, v. This is the velocity of the particle at time t.
(b) The upper graph shows the distance x plotted against time (for a particular motion of the particle. The quantity (x' - x)/(t' - t) is the slope of the line PP' (and is equal to tan y). As t' - t tends to zero, this line becomes the tangent to the curve at the point P (broken line), whose slope is equal to v (=tan y), the velocity of the particle at time t. The lower graph shows the corresponding plot of v against t.
so that its position is specified by one coordinate, its distance x from O. If its coordinate at time t is x, and its coordinate a little time later (t') is x', then the average velocity or speed of the particle in the interval of time from t to t' is v = (x'-x)/(t'-t). This is well defined however short the time interval is; even if we let the interval become so short that t'-t, and hence x'-x, are vanishingly small, v is still defined. The value to which v tends as t'-t tends to zero is the instantaneous velocity of the particle at time t; it is written
 (2.1)
(2.1)
evaluated at time t. The velocity is clearly negative if the particle is moving back towards O, so that x' is less than x.
The definition of dx/dt can be understood graphically from Fig. 2.2 (b)). The upper graph shows how x varies with time t. Representative points P(x, t) and P'(x', t') are marked. The quantity (x'-x)/(t'-t) is the tangent of the angle f between the line joining the two points and the time axis. This quantity is called the slope of that line. As t'-t tends to zero, the point P' moves towards the point P, and the line joining them approaches the tangent to the curve at P (shown in Fig. 2.2 (b) as a dash-dot line). The quantity dx/dt, i.e. v, is thus seen to be the slope of the tangent to the curve at P, and takes the value tan y. The corresponding graph showing how v varies with t is also presented in Fig. 2.2 (b).
The resolution of Zeno's paradox lies in the performance of this limiting procedure; without it there is no way of defining the instantaneous velocity of a particle in terms of its position at successive times. The procedure was in fact not thought of until the seventeenth century, when the calculus was first developed by Newton and Leibniz. In the notation of the calculus, the symbol d/dt represents the rate of change of a quantity with time; in this example, all we mean by dx/dt is the rate at which x changes with time t. The units of velocity must be taken to be consistent with the units chosen for distance and time. If distance is measured in metres and time in seconds, then velocity must be measured in metres per second (m s~1).
The above definition of velocity can readily be extended to situations where the particle is moving in three dimensions. If the fly already referred to were to fly from one corner of the room to the opposite corner, all its coordinates would change with time. The specification of how they all vary would fully determine its motion. The point X of Fig. 2.1 moves along the x-axis with velocity Vx = dx/dt, the point Y moves along the y-axis with velocity Vy = dy/dr, and the point Z moves along the z-axis with velocity Vz=dz/dt. The (three- dimensional) velocity of P is thus fully determined by the three quantities (Vx, Vy, Vz), which are called the velocity components of P, in the x, y, and z directions respectively. They clearly depend on the directions of the coordinate axes, but are independent of the position of the origin O. The total speed at which P is travelling, i.e. the component of its velocity along a line instantaneously parallel to the direction of motion, cannot depend on the directions of the axes. The speed, sometimes called the magnitude of the velocity, can be shown to be equal to (Vx2 + Vy2 + Vz2)1/2, which is a positive quantity even if some or all of Vx, Vy, Vz are negative.
We can specify the velocity of a particle in three dimensions just as precisely by giving both its magnitude and its direction relative to any two of the coordinate axes (for example, if we know the direction of motion of the fly, and its total speed, then its velocity is fully determined). If the magnitude of the velocity is V, and the angles it makes with the x- and y-axes respectively are 0 and 4> (Fig. 2.3),
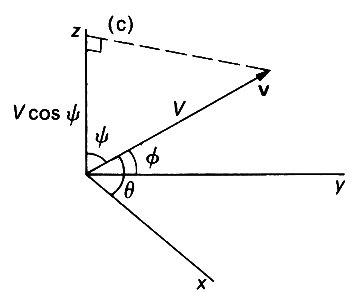
Fig. 2.3. The arrow marked v represents the velocity of a particle, with magnitude V and a certain direction. The component of the velocity in the direction of a coordinate axis is equal to V times the cosine of the angle between that axis and the direction of the velocity. Thus
vx = Vcos q, vy= V cos f, vz = V cos y.
then the components vx and vy are given by
vx = Vcos q, vy= V cos f *
[*The reader is assumed to be familiar with the elementary properties of sines and cosines.]
The third component, vz is then given by
Vz = (V2 - vx2 - vy2)1/2
= V(l - cos2 q - cos2 f)1/2
which is also equal to V cos y, where y is the angle between the direction of the velocity and the z-axis.
The velocity of a particle is an example of a physical quantity which has a certain magnitude and a certain direction. It exists independently of how we choose to measure it, although the value of the magnitude depends on the units used to measure it, and the specification of the direction depends on the orientation of the chosen coordinate axes. Such a quantity is called a vector, and vectors will be represented in this book by symbols in bold type. The velocity of a particle, for example, can then be written by the single symbol v. The quantities (vx, vy, vz) are the components of the vector v, and v can be regarded as equivalent to its three components taken together. We therefore often write v = (vx, vy, vz).
Another example of a vector quantity is the position of the particle P (Fig. 2.1 (b)), which has magnitude equal to the length of OP ((x2 + y2 + z2)1/2), and direction given by the cosines of the angles between OP and any two of OX, OY, OZ; alternatively, its components are the coordinates (x, y, z) themselves. This position vector, say x, is in fact a special type of vector in that it does depend on the position of the origin O; all other vectors describing physical quantities like velocity are independent of the position of the origin. Vector notation, like the use of d/dt for 'rate of change of', is just a convenient form of shorthand. From the definitions of vx, vy, vz as the rates of change of x, y, z (vx = dx/dt, etc.), we can combine the two shorthand notations in an obvious way as follows:
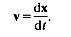 (2.2)
(2.2)
Velocity (a vector) is the rate of change of position (also a vector).
Vectors representing two quantities of the same type (for example, two velocities, or two position vectors) are added together by adding their components. Let x1 = (x1, y1, z1) and x2 = (x2, y2, z2) be two such vectors; then
x1 + x2 = (x1 + x2, y1 + y2, z1 + z2). (2.3)
To see this, consider the situation in two dimensions (Fig. 2.4).
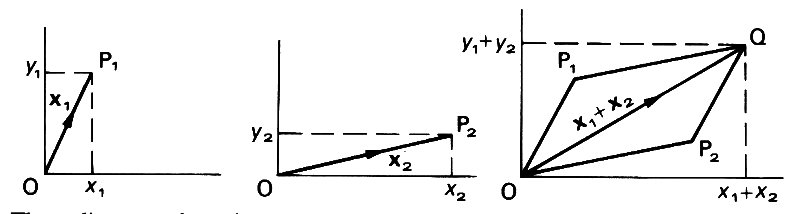
Fig. 2.4. These diagrams show the geometrical interpretation of Equation (2.3) for the addition of vectors, illustrated in two dimensions. The vectors x1 and x2, represented by the lines OP1 and OP2, are added to form the vector x1 + x2, represented by the line OQ. O and Q are the opposite corners of a parallelogram two sides of which are OP1 and OP2.
We add the vector x1 = (x1, y1), representing the point P1, to the vector x2 = (x2, y2), representing the point P2. For the geometric interpretation to remain consistent, the resulting vector should represent the point Q, whose coordinates are (x1 +x2, y1 + y2). This is consistent with Equation (2.3). Alternatively, consider a projectile which, when fired from a fixed point, has velocity v = (vx, vy, vz). Now suppose that the point of firing is itself moving over the ground with velocity U in the x -direction, velocity vector V = (U, 0, 0). Then the velocity of the projectile relative to the ground is increased by an amount U in the x-direction, while its components in the y- and z-directions are unchanged, i.e. v+V=(vx+U, vy, vz).
In the same way as the velocity of a particle is defined as the rate of change of position so the acceleration of the particle, denned as the rate of change of velocity, can also be written down. For motion along a line, the acceleration is dv/dt, which is the same as the slope of the tangent of the graph of v against ( (Fig. 2.2 (b)). It too has three components, the rates of change of the three velocity components, and is also a vector, say a:
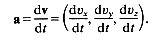 (2.4)
(2.4)
In the notation of calculus, if u = dx/dt, then du/dt can be written d2x/dt2, a useful shorthand for the rate of change of the rate of change of x. Thus we can write
 (2.5)
(2.5)
The units of acceleration must, for consistency, be metres per second squared (ms-2).
It is perhaps a little difficult to grasp the precise definition of acceleration as a three-dimensional quantity. In one dimension, with the particle moving on a straight line OX, it is fairly easy: if the velocity v is increasing at a given moment, then the acceleration a = dv/dt is positive; if v is decreasing a is negative. If the particle is moving back towards 0 with a positive value of x, then v is negative, but if it is at the same time slowing down, the acceleration a is positive. To make it clearer, Fig. 2.5
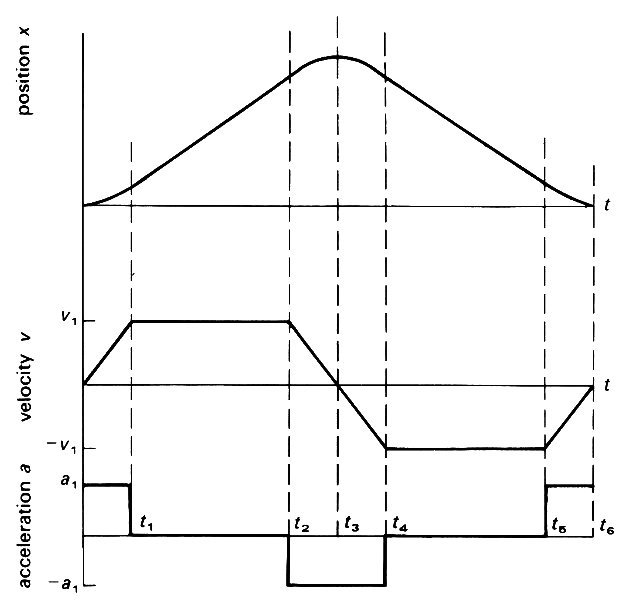
Fig. 2.5. Graphs of distance x travelled along a line, velocity v and acceleration a against time t, for a particle which starts from rest at the origin (x = 0) at time t = 0. Until time t1 it accelerates with uniform acceleration a1 until it has velocity v1. This is maintained until time t2, when the particle acquires a constant negative acceleration -a1 until it has changed direction and is returning towards the origin with the same uniform speed (velocity -v1) at time t4. At time t3, the velocity is zero and the particle is at its farthest distance from the origin. The uniform velocity -v1 is maintained until time t5, and finally the particle is slowed down with uniform acceleration a1 until it comes to rest at the origin at time t6.
shows graphs of x, v, and a against time t for a particle which starts from rest at 0, accelerates up to a uniform speed which is maintained for some time, then decreases speed with constant negative acceleration until it has changed direction and is returning to 0 with the same uniform speed. Finally it is slowed down and stopped at 0 again by the application of a positive acceleration. The direction of the acceleration (the sign of a) is independent of the direction of motion (the sign of u).
In two or three dimensions the direction of the acceleration is also independent of the direction of the velocity. Whenever the velocity is changing, either in magnitude or in direction, the particle experiences an acceleration. For example, suppose that a particle is travelling in a circle with constant speed, like a ball twirled on the end of a string, or a satellite in its orbit round the earth. In this case the magnitude of the velocity is constant, but the particle experiences an acceleration because the direction of the velocity is changing (Fig. 2.6).
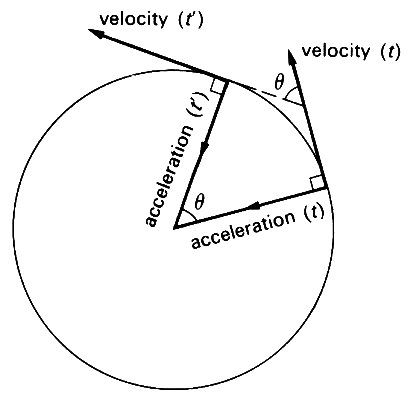
Fig. 2.6. A particle moving in a circle of radius r with constant speed u experiences an acceleration of magnitude v2/r towards the centre of the circle. The angle q is the angle swept out by the line from the centre to the particle in the time from t to t'.
Since the speed is constant, this acceleration must be in a direction perpendicular to the direction of motion (otherwise there would be a component in the direction of motion, and the total speed would change), and therefore the direction of the acceleration passes through the centre of the circle. If at time t the velocity (magnitude v) is in a certain direction, then a little time later (t') it will have acquired a component in the perpendicular direction because of the acceleration, and the velocity vector will point in a different direction. The component of velocity acquired in the time t' - t is equal to v times twice the sine of 1/2q, which, when q is very small, is equal to the distance traversed by the particle in that time, v x (t' - t), divided by the radius of the circle r. Thus the perpendicular component of velocity is v2(t' - t)/r, and its rate of increase, when t' - t tends to zero, is v2/r, which is the magnitude of the acceleration towards the centre. A planet travelling round the sun, or a satellite travelling round the earth, experiences an acceleration towards the sun or the earth respectively. Similarly a particle of blood streaming round the curved arch of the aorta must experience an acceleration towards the centre of curvature.
We are now able to describe the position, velocity, and acceleration of a particle as it moves on a given path in space. But what causes particles or bodies to move or stop moving? The answer is forces. It is unfortunately difficult to give a precise definition of force, although we all have a qualitative idea of its nature from everyday experience. From a logical point of view, the argument we shall give is a circular one, since we say that force causes motion, but is defined by the motion it causes. Nevertheless, the argument is scientifically respectable because it incorporates the results of simple experiments which remove all ambiguity.
If we lift a heavy weight, we use more force than if we lift a light weight. If we wish to prevent a car rolling downhill we have to exert a force in the uphill direction. We can stop a ball rolling along a table by applying a force to it, and if no force is applied it goes on rolling. We do not need to involve the mysterious force which the Greeks thought was required to maintain a body in motion, since we can recognize that a moving body will remain in motion with a constant velocity unless a force is exerted to change that velocity. A much more satisfactory explanation of everyday experience can be obtained, as Newton showed, if forces are associated with changes in velocity, or accelerations, and not with velocity itself. Zero force is associated with zero acceleration, i.e. with constant velocity (which is itself zero if the body is at rest).
What, then, is the relationship between force and acceleration? If two balls, one heavier than the other, are rolling with the same velocity on a flat horizontal surface, and if we wish to stop them over the same period of time (i.e. give them the same negative acceleration), we have to exert a larger force on the heavier ball. The quality possessed by the heavier ball which makes it more difficult to stop it or give it positive acceleration is called inertia, and in this book we shall use this word in a purely qualitative way. The quantity which represents the inertia of a body is its mass, which is a measure of the total amount of matter in the body. A body with greater mass is more difficult to accelerate (or decelerate); similarly it is its greater mass which causes one object to be heavier, i.e. have a greater weight, than another. The unit of mass is independent of the units of length and time, and the three together form a fundamental system of units in terms of which all other mechanical quantities are measured. We shall use the kilogram (kg) as the fundamental unit of mass, although some quantities will be given in grammes (1 g = 10-3 kg) (see Chapter 3).
The precise relationship between force, mass, and acceleration, from which the definition of force will become clearer, is given by Newton's laws of motion, which are set out below.
(i) First law. Every particle continues in a state of rest or of uniform motion in a straight line unless acted on by some external force or forces. In other words, the velocity v remains constant, maybe zero, if no net force (see below) is acting.
(ii) Second law. When a particle of mass m is acted on by a force or forces so that it experiences an acceleration a, the net force acting on it is equal to the mass multiplied by the acceleration. In other words, the net force is a vector, which we may call F, given by
F = ma. (2.6)
This equation is often called the equation of motion of the particle.
By net force we mean the sum of all forces acting on the particle, which may be exerted in different ways. For example, if we push an object along a horizontal table (Fig. 2.7),
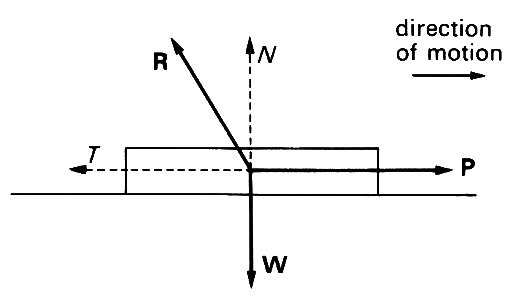
Fig. 2.7. Diagram representing all the forces acting on a body being pulled horizontally along a flat table to the right. P is the force pulling it, W is its weight, and R is the force exerted on the body by the table. R has two components, one vertically upwards (N), which would be present even if the body were just resting there, and a frictional component T in the direction opposite to the direction of motion.
the forces on it include the gravitational attraction of the earth (i.e. the weight of the object, W), the force R exerted by the table on the ball (which will in general include a component holding it up, N, and a frictional force T in the direction opposite to the direction of motion) and the forward force P (which we are exerting directly). If the forward acceleration is a,then
P + R + W = ma. (2.7)
Addition of forces is carried out by the addition of their components as in Equation (2.3). Thus if we choose x- and y-axes fixed relative to the table as shown (supposing the z -direction to be out of the paper), and if P = (P, 0, 0), R = (-T, N, 0), W = (0, - W, 0) and a = (a, 0, 0), then Equation (2.7) becomes
(P-T, N-W, 0) = (ma, 0, 0).
Clearly, two vectors can be equal only if each component is equal; we deduce that N - W = 0 (i.e. the upward force exerted by the table on the object is equal to its weight, so that there is no vertical acceleration), and P - T = ma, which relates the horizontal component of force to the acceleration of the body.
From Equation (2.6) we deduce the unit of force: since mass is measured in kg, and acceleration in m s-2, force must have the unit kg m s-2 (kilogram metre per second per second), which is appropriately called the newton (the weight of an average apple is about 1 newton). As we shall discuss in more detail later (Chapters 3 and 6), it is important that the quantities used in any equation, such as Equation (2.6), should be given the correct units. Indeed, a useful way of testing the consistency of an equation is to verify that the terms on either side of it are measured by the same units. For example, a length can never be equal to an area, nor a velocity to an acceleration, nor a force to a mass; an equation in. which such equalities were stated would be not only wrong but meaningless too.
(iii) Third law. To every action there is an equal and opposite reaction. That is, if one body exerts a force (F) on another body, the second body must exert an equal and opposite force (-F) on the first body. So in the example of Fig. 2.7, the fact that the table exerts an upward component of force N and a retarding component of force - T on the body means that the body exerts a downward force -N and a forward force T on the table. If you catch a ball by applying a force to it, you are aware that the ball applies an opposite force to you. When you hold a heavy weight, you have to exert an upward force on it because it is exerting a downward force on you; you also exert a downward force on the ground, which again reciprocates.
The types of force which are present in the example of the object on the horizontal plane surface (Fig. 2.7) are of two kinds, long-range and short-range.
First there is the weight of the body, which is an example of the gravitational attraction exerted between any two bodies with mass. In this case one body is the earth, and the long-range force exerted by it on a particle of mass m near its surface (the weight of the particle, W) is directed approximately towards the centre of the earth (i.e. vertically downwards), and is proportional to m. Its magnitude varies only slightly with position on the earth, and can be regarded as constant in any local experiment. So we can write
W = mg (2.8)
where g is a vector whose magnitude is a constant, and which is directed vertically downwards. A comparison of Equations (2.8) and (2.6) shows that g has the dimensions of acceleration, and use of Equation (2.6) shows that a body falling freely, when the only force acting is its weight, will experience the downward acceleration g. We call g the acceleration due to gravity; its magnitude g is approximately 9.8 m s-2. The approximate constancy of g gives rise to a convenient way of measuring the mass of a body, that is by comparing its weight with that of a given standard body, which itself need not be measured at the same time or place.
Gravitational attraction is a long-range force, in that it is exerted on any given particle by all other particles, whether they are in contact with it or not. Another example of a long-range force is the force a moving charged particle experiences in an electric or a magnetic field.
The other forces acting on the body in Fig. 2.7 are short-range forces, which can be exerted by two bodies only when they are in contact. P is the force applied by us by direct pushing or pulling. R, the force exerted by the table, would not exist if the bodies were not in contact. Its normal component N exists because the body and table are pressing together, and a similar force is present wherever two bodies are in contact (when you touch something, you feel it because it exerts a normal force on you). The tangential component T of R is a frictional force, which would be absent if the bodies were perfectly smooth. For two given surfaces in relative motion, T is usually proportional to N (T = CN), the constant of proportionality C being called the coefficient of friction. If the applied force P is less than CN, the body will not move (a = 0), and the actual frictional force T is just enough to prevent movement, i.e. is equal to P. We shall see below that the forces exerted on the 'particles' of a continuous deformable material can also be divided into long-range and short-range forces of a similar kind.
The whole of mechanics follows from Newton's three laws. Before we develop their application to continuous fluids or solids, it might be helpful here to see a couple of examples of their use in the motion of particles (or of the centres of mass of large bodies, which are equivalent).
(i) If a man is driving a car, total mass M, at velocity V, and wishes to stop it, he usually causes the brakes to exert a fairly uniform retarding force F in the opposite direction, so that his acceleration is F/M (Newton's second law, Equation (2.6)); the component of F in the direction of motion is of course negative, causing deceleration. The driver (mass m) remains at rest relative to the car, because he exerts a small forward force on it (through his legs and the pedals, his arms and the steering wheel, etc), causing it to exert a backward force of the same magnitude on him (Newton's third law). This magnitude must be m/M times the magnitude of F in order that the driver should experience the same deceleration as the car. If the retarding force F is large and applied very suddenly (e.g. if the car hits a tree), the driver may be unable to exert a large enough force on the car in the usual way to cause it to give him the same deceleration as the car. He will continue forward, relative to the car, until stopped by something which can supply the necessary force (e.g. his chest against the steering-wheel, or seat-belt).
(ii) Consider a particle (mass m) travelling in a circle with constant speed (Fig. 2.8 (a)).
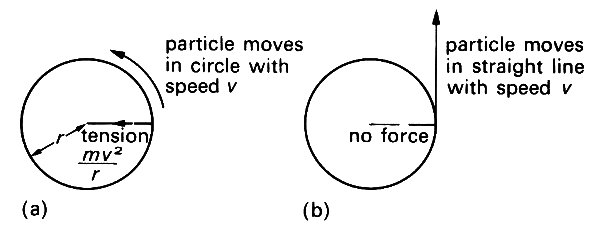
Fig. 2.8. (a) A particle is attached to a string of fixed length and moves in a circle of radius r with speed i). The tension in the string must be equal to the mass of the particle (m) times the acceleration which it experiences towards the centre of the circle (v2/r). (b) When the string breaks, no force acts on the particle, and it moves oft in a straight line with speed v.
We have seen that it experiences an acceleration towards the centre of the circle. Therefore, by Newton's second law, there must be a force acting on it in the same direction. If the particle represents a ball on a string, the force is supplied by the string, and is called the tension in the string.* [*This tension is the total force exerted by the string on the ball, and in mechanics the word always represents a force. It should not be confused with the tensile stress experienced by the material of which the string is made, since this is the force per unit cross-sectional area (see Chapter 7). Nor should it be mistaken for the surface tension in a film or membrane, which is the force exerted by such a surface per unit length of its boundary. Also the use of the word 'tension' to describe the partial pressure of a gas in solution is misleading, and should be abandoned.]If it represents a planet moving round the sun, the force is gravitational. The magnitude of the force is equal to m times the magnitude of the acceleration, i.e. is mv2/r, where v is the speed of the particle, and r the radius of the circle.
If the force suddenly stops (e.g. if the string breaks) the particle can no longer experience any acceleration, and therefore flies off in a straight line at a tangent to the circle, with constant velocity, until acted on by another force (Fig. 2.8 (b)). This flying off has sometimes led people to suppose that a particle moving in a circle is acted on by an outward force, called the centrifugal force, which is balanced during circular motion by the tension in the string; and that when the string breaks, this force causes the particle to leave its circular orbit.
Such a view is misleading, and should be avoided: a broken string exerts no force. Another example of bodies moving in circles is supplied by manned artificial satellites. Here both the satellite and the men in it are travelling in the same circular orbit, which we may take to have radius r, with the same speed (say, v). Thus they each experience the same acceleration, v2/r, towards the centre of the earth, and each object must experience a force in that direction equal to v2/r times its mass. This force is supplied by the earth's gravitational field, which exerts a force on any body proportional to its mass', and inversely proportional to its distance from the centre of the earth (i.e. F = km/r2, where k is a constant and m the mass of the body). Thus Newton's second law can be applied to any object in the given orbit, to give
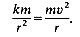
So as long as k = v2r, any object can travel in that orbit without any additional force being supplied. Thus no force is applied between a man inside the capsule and the capsule itself, as long as the man is not moving relative to the capsule. He experiences weightlessness, in that as he floats about inside the capsule he experiences no force tending to bring him in contact with the 'floor' of the capsule. The same goes for the blood in his circulation. For any particle of blood, there is a balance between the earthward force, and the earthward acceleration resulting from its circular motion. This causes considerable physiological problems, because man has evolved in an environment where gravity is always experienced. A man on a space walk outside the capsule is in the same circumstance as a man inside. No extra force need be applied to him as long as he remains at rest relative to the capsule. Nor is there any air resistance or other force tending to slow him down relative to the capsule, so he does not require a counteracting tension in the lines holding him to it. These lines therefore do not become stretched out as they would within the earth's atmosphere, where the drag of the air is important.
There are one or two more mechanical terms which should be defined before we outline the application of Newton's laws to continuous materials.
The second law states that force equals mass times acceleration, i.e. mass times (rate of change of velocity). This can just as easily be written as the rate of change of (mass times velocity), as long as the mass is constant; in symbols:
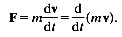 (2.9)
(2.9)
It is this form of the equation which is in fact the more general, because it can be applied to the motion of bodies whose mass is changing, like a rocket which burns fuel and shoots it out behind. The quantity mv is called the momentum of a particle, and Newton's law can be expressed in the form 'Force equals rate of change of momentum'. In the absence of external forces, the momentum of a particle, or of a body or system of particles, remains constant, or is conserved. For example, if two particles (masses m1, m2; velocities v1, v2) collide and coalesce, the combined body, mass (m1+m2), must have the same momentum as the two original bodies put together, so its velocity must be (m1v1+ m2v2)/(m1+m2). If the collision were instantaneous, this would be true immediately afterwards even if external forces (e.g. gravity) were acting, because there would be no time for the total momentum to be changed during the collision. If a car of mass M is travelling at speed V in a certain direction, say the .x-direction, so that its velocity vector is (V, 0, 0), and a lorry of mass 10M is travelling in the opposite direction with speed 1/10V, velocity vector (1/10V, 0, 0), the total momentum of the two is zero, and their centre of mass is at rest. It would remain at rest if the two vehicles collided, although the motion of the two vehicles relative to their centre of mass would change dramatically.
When a force of magnitude F is applied to a particle while it travels a distance d in the direction of action of the force, then the force is said to do work, and the amount of work done is equal to Fd. This result also holds when the force and the direction of motion are not parallel (Fig. 2.9);
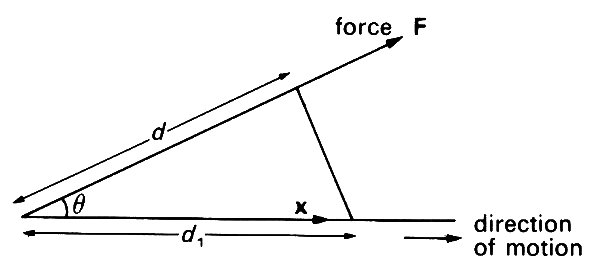
Fig. 2.9. The work done by a force of magnitude F acting on a particle which moves a distance d i in a straight line is equal to Fdi cos 6, where 0 is the angle between the direction of the force and the direction of motion. This is the same as Fd, where d (= d\ cos 6) is the projection of rfi on the direction of action of the force. It is often written F. x, where F is the vector force, and x is the position vector of the end of the path travelled, relative to the beginning.
d is then the projection of the distance travelled on the direction of the force. Alternatively, the work done is equal to the component of force in the direction of motion (F cos q in Fig. 2.9) times the distance travelled d1; this is the same as Fd since d = d1 cos q. If F = (F1, F2, F3) is the force, and the position of the end of the path relative to the beginning is x = (x1, x2, x3), the work done can be shown to be (F1x1 + F2x2 + F3x3), which is commonly written F • x. If F is not constant, or if the direction of motion is variable, then the path of the particle has to be split into small straight segments over which F is constant, and the total work done is obtained by adding together the work done over each segment.
For a body moving in a circle with constant speed, like a ball on the end of a string (see §2.4), the force acting on it is directed towards the centre of the circle, and is always at right angles to the direction of motion. It therefore does no work.
It can be shown, from Newton's second law, that the total work done on a particle, over a period of time, by all the forces acting on it, is equal to the change in the quantity 1/2mv2, where m is the mass of the particle, and v is its speed. This quantity is called the kinetic energy of the particle. If we apply the quoted result over a very short time, we obtain the additional result that the rate at which forces do work on the particle is equal to the rate of increase of its kinetic energy at any instant.
When the particle moves in the earth's gravitational field, the gravitational force on it is mg vertically downwards; if the z-axis is taken vertically upwards, this force has components (0, 0, -mg). We can now define a quantity mgz, called the potential energy of the particle. The work done per unit time by the gravitational force is (-mg) dz/dt, which is equal to —d/dt (mgz), i.e. minus the rate of change of potential energy. In the absence of other forces this must be equal to the rate of change of kinetic energy. In other words the rate of change of total energy (kinetic plus potential) is zero; this result is called the principle of conservation of energy.
Kinetic energy + potential energy = 1/2mv2 + mgz
= E, a constant. (2.10)
The value of E is arbitrary, since it depends on the origin of coordinates (the level at which z is taken to be zero), but once that has been chosen, E remains fixed. A body possesses kinetic energy by virtue of its motion, while its potential energy is determined by its position. Suppose that during motion under the action of no force but gravity a body loses height, i.e. that its potential energy is reduced. The principle of conservation of energy then shows that the kinetic energy of the body, and hence its speed, must increase. Similarly, if the body rises, it must lose speed.
Potential energy can be thought of as stored energy, which may be transformed into kinetic energy (i.e. motion) when it is released. There are numerous ways of storing energy other than by raising a body in a gravitational field. The most important from the point of view of cardiovascular mechanics is by stretching (or compressing) an elastic material. When a particle is attached to a spring which is stretched and then released, the stored potential energy is converted into kinetic energy, and the particle moves. Similarly if a balloon is blown up to a high pressure, and the nozzle is then released, the air rushes out; i.e. the potential energy stored in the stretched rubber is converted into kinetic energy of the air. The same is true of blood vessels, which become distended when the local blood pressure is high, but contract again, contributing to the motion of the blood, when the pressure falls again (see Chapter 12).
Elastic forces and gravity have the property that when a body is caused to move against them, then the work done is stored as potential energy, and is subsequently recoverable as kinetic energy. Then the principle of conservation of energy holds, and the forces are called conservative forces. Not all forces are conservative. In particular, forces of a frictional nature, like friction between two solids sliding on each other (as in the example on p. 15), or air resistance, are such that any work done against them is lost as mechanical energy. Mechanical energy is not conserved but is dissipated (in fact it is converted into heat), and these forces are known as dissipative forces. When dissipative forces are acting, the principle of conservation of mechanical energy does not hold. However, if the mechanical energy lost by dissipation can be shown to be small compared with the otherwise conservative energy changes expected in a given motion, then dissipation can be neglected in a calculation with little loss of accuracy in the results.
As an example of the use of the energy principle, consider a ball thrown up into the air, and suppose that the only force acting is its weight (i.e. neglect air resistance). If the ball is released with upwards speed V, from a certain level which we may take to be z = 0, then its subsequent speed v is related to its height z above that level by Equation (2.10). The values of the constant E are given by the conditions at release where z = 0 and v = V; thus E == 1/2mV2 and Equation (2.10) give
gz + 1/2v2 =1/2V2. (2.11)
Note that there is no horizontal component of the motion, because the horizontal component of velocity is zero initially, and there is no horizontal force. From Equation (2.11) we can calculate the maximum height attained by the ball, since at that height (z = h, say) its velocity must be zero (v = 0). Hence
h = V2/2g. (2.12)
Similarly, the downward velocity of the ball when it returns to its point of release (z = 0) again has magnitude V: on the way up, the velocity vector had components (0, 0, V), while on the way down it has components (0, 0, -V).
It can readily be verified that Equation (2.12) is dimensionally correct, since V is a velocity (m s-1) and g is an acceleration (m s-2), so that the units of V2/2g are
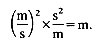
Thus V2/2g has the units of length. The unit of energy is that of a mass times the square of a velocity, i.e. is kg m2 s-2; this is of course the same as the unit of work (force times distance). The unit of momentum (mass times velocity) is kg m s-1.