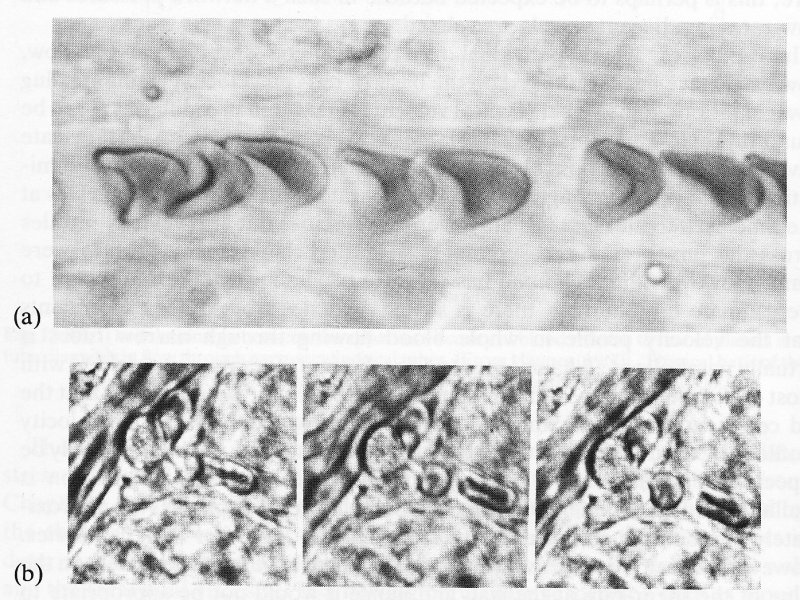
Mammalian capillaries range in diameter from 10 mm down to 3 mm, so that blood cells, in particular red cells, have to flow down them in single file. In capillaries whose diameter is less than the diameter of a red cell (7-8 mm) the cells must be deformed in order to pass through the vessel. Observation shows that normal red cells take up various configurations within small capillaries; some are bent back in an approximately symmetrical parachute shape (Fig. 13.33, panel a), while others may roll up and flow down the vessel end on panel b. As we have seen, the shape of a normal cell permits considerable distortion without change of either volume or surface area (see §10.3.2). Abnormal cells which are hardened or are almost spherical cannot be deformed so easily and therefore cannot pass through the smallest vessels.

Fig. 13.33. Photographs of the configuration of red cells flowing in small capillaries, (a) Parachute configuration, (b) Rolled up, flowing end on. (From Skalak and Branemark (1969). 'Deformation of red blood cells in capillaries'. Science, N.Y. 164, 717-19.)
Experiments have been performed in which red cells were made to pass through membranes containing pores of different sizes. It is found that normal cells can pass through undamaged when the pore diameter is greater than 3 mm, but that they are damaged when forced through smaller pores (Fig. 13.34). Cells which are artificially hardened or are made to swell into a spherical shape by osmotic means, both of which make them less flexible, cannot pass through pores less than 8 mm in diameter without haemolysis.
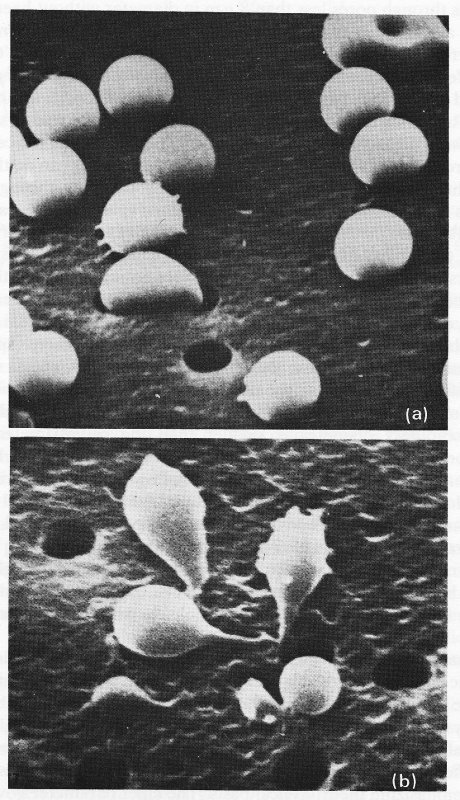
Fig. 13.34. (a) and (b) Scanning electron micrographs of red blood cells (a) before and (b) after passing through a polycarbonate sieve of pore diameter 2.2 mm. In (a) many of the cells appear spherical because they have already partially entered the pores. (From Chien, Luse, and Bryant (1971). 'Hemolysis during filtration through micropores: a scanning electron microscopic and hemorheologic correlation'. Microvasc. Res. 3, 197-8.)
There is a hereditary disease of humans, called hereditary spherocytosis, in which the red cells are spherical and have a diameter of about 6 mm. The patient suffers from excessive haemolysis, so that, although red cell production is increased several fold, it cannot keep pace with cell destruction, and anaemia develops. Removing the spleen improves the situation. The reason seems to be that, in flowing through the capillaries in the splenic pulp, the red cells have to squeeze through gaps as little as 3 mm across. Normal cells can do this without excessive haemolysis, in the same way as they can pass through artificial micropores of similar diameter, but the abnormal spherical cells cannot.
In describing the mechanics of red cell motion in narrow capillaries, we can distinguish two situations according to the ease with which the cells fit into the vessels. First, when the capillary has a diameter noticeably larger than that of the cell, the cells can fit into the tube without distortion (there is positive clearance), and suffer little or no distortion as they flow in single file along it. In this case, the pressure in the plasma is comparable everywhere (apart from a more or less uniform pressure gradient driving the flow), and is unlikely to cause significant distortion of the cells. Therefore the deformability can be neglected in an analysis of the dynamics. The second and more usual case arises when the capillary diameter is smaller than the cell diameter (negative clearance). In this case the cell has to be deformed in order to fit into the capillary, and suffers further distortion as it flows. High pressures must be generated locally in the thin layer of fluid round the edge of the cell in order to deform it, and therefore depend on the elastic properties of the cell (and of the capillary wall, although that is considerably stiffer than the cell). The whole flow pattern is dictated by the motion in these thin regions of high pressure, which can be analysed by the methods used in the theory of hydrodynamic lubrication (outlined in §13.6.2). We shall consider the two cases separately.
13.6.1 Positive clearance. In this case the detailed shape and spacing of cells, as well as their elastic properties, are relatively unimportant. The main feature of the flow can be understood by considering a simple model in which the cells are replaced by rigid spheres, flowing steadily and symmetrically in single file down a cylindrical tube (Fig. 13.35). A mathematical analysis can be carried out for this simplified geometry, and we shall summarize the numerical results of this analysis, emphasizing their physical basis. The chief parameter governing the motion, given that inertial forces can be neglected, is the ratio of the radius b of the sphere to the radius a of the tube. The way the relative velocity of the spheres and the fluid depends on this ratio can be illustrated by the two existing cases, in which b/a is very small and in which it is equal to 1. In the former case, which is physiologically unrealistic, the spheres do not significantly affect the fluid motion, which is Poiseuille flow. Because they are situated on the centre line, they have a velocity equal to twice the average velocity of the fluid. As b/a is increased, the ratio between the particle velocity and the average velocity of the flow falls, approaching the value 1 as b/a approaches 1. In this extreme case the particles fill the tube, and the fluid cannot pass around them, being carried along in 'boluses' between the particles. Except in this extreme case, however, the particles travel faster than the fluid (resulting in a reduced dynamic haematocrit, as discussed in §13.5.7). This result implies that, relative to the particles, there is a 'leak back' of fluid which drives a circulatory motion in the 'bolus' of fluid carried along between them (Fig. 13.35).
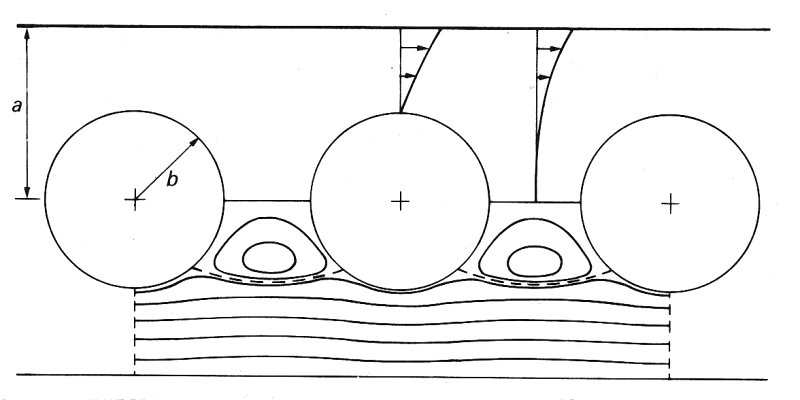
Fig. 13.35. Streamlines and velocity profiles for flow of rigid spheres down a rigid tube. Observer is moving with spheres so that they appear fixed and walls move. (From Wang and Skalak (1969). 'Viscous flow in a cylindrical tube containing a line of spherical particles'. J. Fluid Mechan. 38, 88.)
Another important result is that the ratio of the pressure drop required to push the suspension of spheres down a narrow tube at a given flow-rate, to the equivalent pressure drop for the suspending fluid alone, increases with increasing radius ratio b/a. For example, when (1) b/a = 0-9 and (2) the spheres are touching (which gives the greatest excess pressure drop for a given b/a), the ratio reaches a value of about 2: i.e., the total pressure drop for fluid plus spheres is about twice the fluid-only pressure drop. This implies that the apparent viscosity, of the suspension is approximately twice that of the suspending fluid.
If we were to apply this result to blood in a capillary, we would predict its viscosity to be about twice that of plasma. In fact we know that the viscosity of whole blood as measured in a large-scale viscometer in bulk is about three times that of plasma (§10.6.3), so the Fahraeus-Lindqvist effect (§13.5.1) is shown to operate even when b/a is as large as 0.9 (Fig. 13.32).
13.6.2 Negative clearance. In this case the red cells have to pass down capillaries narrower than themselves. The cell must be squashed in order to fit into the tube whether it is moving or not. When it is at rest, it is jammed up against the vessel wall, or at least against the mucopolysaccharide layer which lines the wall. When the cell starts moving, under the action of a pressure gradient, there must be slip between it and the vessel wall, resisted by frictional or viscous forces. It is a matter of common experience that the frictional forces between two slipping surfaces are greatly reduced, once the motion has begun, by the introduction of a layer of fluid between the surfaces. This is the lubricating layer. The most convincing theoretical model of red cell motion in narrow capillaries is one in which such a lubricating layer is formed round the cell, and we here outline the principal features of this model, and report its main physiological predictions.
We have seen that red cells can take up a number of different orientations as they flow along narrow capillaries, but we do not know which arise most commonly. They are all very difficult to analyse, and the only one for which an approximate quantitative theory has been developed is the axisymmetric parachute configuration. The physical principles underlying the motions are the same in each case, but the details of the pressure distribution around the red cell, for example, will be different.
Because the elasticity of the deformed cell tends to squeeze it against the vessel wall, there must be a relatively high pressure in the lubricating layer of plasma in order to keep the two surfaces separate. This is one of three factors which are crucial to a correct mechanical explanation of the motion. The second is that fluid within the layer must move in such a way that the pressure gradient and viscous forces within it are in balance. Thirdly, the net pressure force acting on the cell must be in balance with the total viscous retarding force on it.
In analysing the motion of the cell and of the plasma in the lubricating layer, it is convenient to suppose that we, the 'observers', are travelling at the same speed (U) as the cell (Fig. 13.36). The cell then appears to be at rest, and the capillary wall moving backwards with speed U. This is convenient because only if we move with the cell do the pressure and layer thickness appear constant in time.
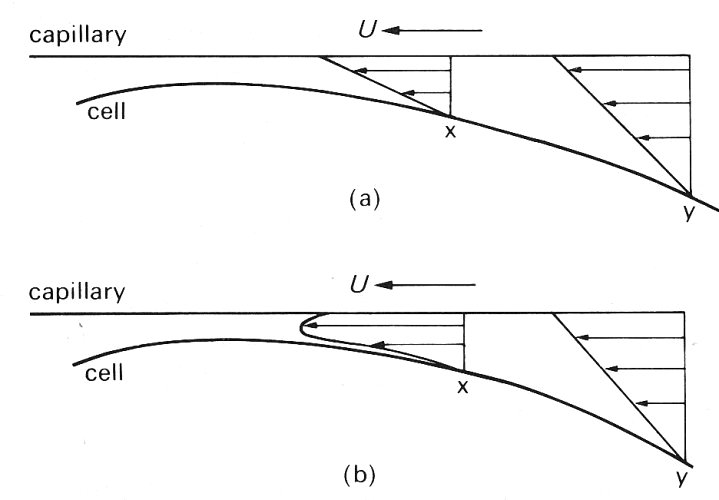
Fig. 13.36. Diagram showing the need for leak back past a red cell in a capillary (cell taken to be at rest, capillary wall moving), (a) Linear profile everywhere leads to non-uniform flow-rate, which is not permitted, (b) Continuity upheld by the superposition of a parabolic component, requiring a pressure gradient.
A consideration of the flow within the lubricating layer shows that there must be leak-back of fluid past the cell in this case too. If there were no leak-back, the velocity profile everywhere would be linear (Fig. 13.36 (a)); and, since the layer is thinner at X than at Y, the volume flow-rate would be smaller there. That is impossible in an incompressible fluid and hence the profile cannot be everywhere linear; there must also be another component as shown in Fig. 13.36 (b), and this in turn implies the existence of a backward (i.e. positive) pressure gradient. If the volume flow-rate associated with this departure from the linear profile is Q, and if x is the distance measured along the capillary wall from left to right, then the force balance in the layer requires that the pressure gradient (dp/dx) at a point where the layer thickness is h is the sum of two terms, one positive and proportional to Q/h3, and the other negative, proportional to - U/h2. The pressure gradient is given by
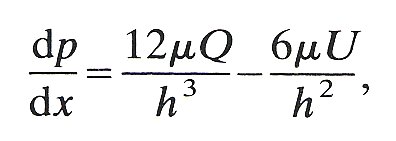 (13.2)
(13.2)
where m is the viscosity of plasma. It is the detailed analysis of the force balance leading to this equation which is called 'lubrication theory'.
The nature of the pressure distribution can now be predicted qualitatively as follows, with reference to Fig. 13.37. The pressure far upstream of the cell, p+, is greater than that far downstream, p-, since the average pressure gradient must be a favourable one (i.e. negative), as in the absence of cells. Far away from the cell the thickness of the lubrication layer becomes large and Equation (13.2) shows that the pressure gradient must be negative (since 1/h3 is much smaller than l/h2). However, at or near the position where the cell would have maximum diameter if it were not distorted by the tube, the point X in Fig. 13.37, there must be a pressure maximum because it is there that the cell has to be squashed the most. Just upstream of that pressure maximum the pressure gradient is positive, and there must be a minimum of pressure yet further upstream (the point Z) for consistency with the negative pressure gradient far away. Thus the pressure distribution must be shown in Fig. 13.37 (a). Equation (13.2) indicates that the minimum layer thickness is associated with the maximum positive pressure gradient, and should therefore occur at the point Y (Fig. 13.37 (b)), further upstream than the minimum layer thickness in the absence of flow.
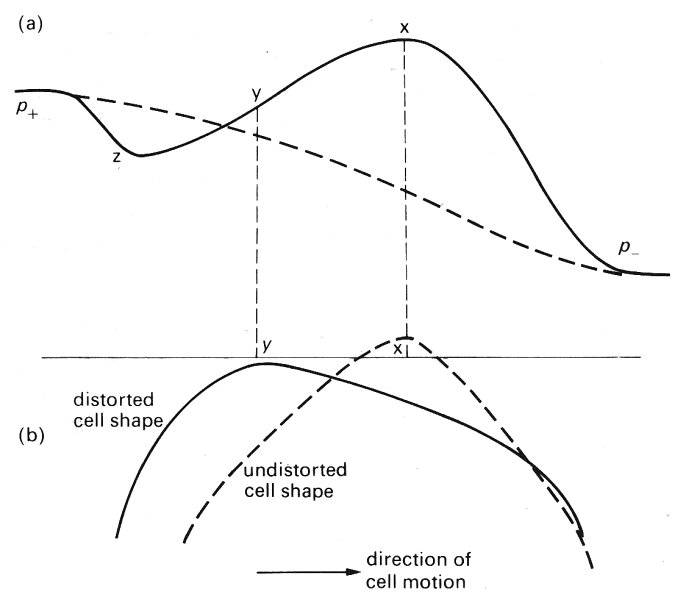
Fig. 13.37. (a) Approximate pressure distribution in the thin lubricating layer of plasma between red cell and capillary wall, and (b) approximate shape of the distorted red cell. Broken line in (a) shows approximate pressure distribution in tube in absence of cell.
These qualitative predictions are borne out by calculations which incorporate detailed information about the elastic behaviour of red cells. The calculations also lead to the following conclusions, which can in principle be tested by physiological experiment.
(i) For a given overall pressure gradient, the volume flow-rate is much smaller than for plasma-filled tubes (in contrast with the case of positive clearance).
(ii) The cell velocity depends non-linearly on the overall pressure gradient, decreasing very rapidly (proportional to the square of the pressure gradient) as the pressure gradient tends to zero.
(iii) For a given positive clearance, the thickness of the lubricating layer is relatively insensitive to velocity.
(iv) When the clearance is negative, the layer thickness decreases as the velocity (or pressure gradient) decreases; it is proportional to the pressure gradient as that tends to zero.
From this last result we conclude that if the pressure gradient or velocity becomes small enough, the lubricating layer of plasma will become so thin (a few molecules across) that it no longer acts like a continuous fluid layer, and loses its lubricating properties. The layer may be supposed to 'seize up' and flow to stop. It would require a very much higher pressure gradient to overcome solid friction and restart the motion after seize-up than was required just before.
As yet it has not proved possible to confirm all. these predictions by physiological measurement. It is known that the resistance to blood flow through capillaries is larger than predicted for a Newtonian fluid with viscosity equal to the viscosity of whole blood in bulk. This effect is the reverse of the Fahraeus-Lindqvist effect apparent in larger tubes, and is in agreement with (i) above. It has also been verified in model experiments that there is a non-linear relationship between pressure gradient and cell velocity, but physiological evidence is still conflicting. In particular it appears that the prediction of seize-up of the lubrication layer is not borne out in vivo. One possible explanation is non-Newtonian behaviour of the plasma, which may be important because the predicted layer thickness at seize-up is less than 0.5 mm and is therefore comparable with the diameter of the largest plasma protein molecules. (The layer of mucopolysaccharide on the endothelial surface may also be involved.) Another explanation may be that the assumptions made about red cell elasticity are inadequate.
Both the high pressures in the lubrication layer, and the circulating motions in the 'boluses' of plasma between cells, may have an influence on mass transfer between the blood and the capillary wall.
For a long time it was considered that the transport of materials from blood to tissue, and in the opposite direction, took place exclusively across the walls of the capillary vessels. However, it is now clear that transport is not thus confined, but occurs mainly in both the capillaries and the post capillary venules in most microcirculatory beds. Thus in this section we shall consider transport in and out of both types of vessel though often the actual vessel being considered will not be defined and the term capillary used. The reader is referred to Chapter 9 for a general discussion of mass transfer.
Transport across the capillary wall does not usually appear to be active in form, because poisons such as potassium cyanide have no direct effects on transport rates. There are two principal mechanisms of transport; bulk fluid movement under the action of a hydrostatic pressure gradient, and transcapillary molecular exchange, a diffusional process driven by a concentration difference across the vessel wall. An enormous range of types and sizes of molecules cross the wall, including water, dissolved gases such as oxygen and carbon dioxide, low molecular weight ions such as Na+ and HCO3-, and organic molecules whose sizes range from a molecular weight less than 60 (urea) to several millions (certain lipoproteins). A number of different pathways and mechanisms for transport exist and these will be considered in the following sections.
Whilst the two principal mechanisms of bulk and diffusional transport are independent, transport rates are linked because the driving pressure and concentration differences are related through osmotic effects, since the vessel wall acts as a semi-permeable membrane.
13.7.1 Filtration and re-absorption of water within single capillaries. It was widely appreciated in the nineteenth century that the hydrostatic pressure difference across the capillary wall is capable of transporting water from the blood into the surrounding interstitial space. However, it was another of Starling's great achievements in 1896 to realize that this filtration pressure is counteracted by a resorptive force due to the presence of protein in the plasma. Starling considered that the capillary wall was permeable to water, electrolytes, and very small molecules within the plasma, but not to protein molecules. Consequently as the water and electrolytes were filtered out of the plasma, an osmotic imbalance was established and a colloid osmotic pressure difference was set up opposing filtration. Thus if the hydrostatic pressures within the capillary and tissue were pc and pt respectively and the colloid osmotic pressures in the two compartments were Pp and Pt, then the net filtration force (DpF) would be given by
DpF = (pe - pt) - (Pp - Pt) (13.3)
When DpF is positive (i.e. when the hydrostatic pressure difference is greater than the osmotic pressure difference) filtration of fluid out of the capillary occurs. When DpF is negative re-absorption of fluid from the interstitial space into the capillary will take place. Starling proposed that the interstitial space could be considered to possess an effectively uniform hydrostatic pressure p, and colloid osmotic pressure P,. Thus it was considered that at the arterial end of a capillary the capillary hydrostatic pressure was greater than plasma oncotic pressure; as a result filtration out of the vessel took place (Fig. 13.38).
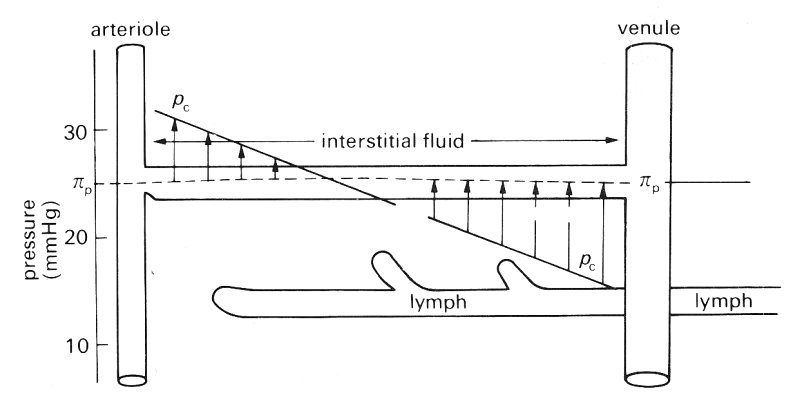
Fig. 13.38. Schematic diagram of a typical capillary to illustrate the filtration-absorption hypothesis of Starling. Capillary pressure pc tails along the length of the vessel; capillary oncotic pressure lip is also shown. (After Landis and Pappenheimer (1963). 'Exchange of substances through the capillary walls'. In: Handbook of physiology. Section 2: Circulation vol. II (ed. Hamilton and Dow), pp. 961-1034. American Physiological Society, Washington D.C.)
At the venous end of the capillary the hydrostatic pressure within the capillary would have fallen and the plasma oncotic pressure would have become elevated above the hydrostatic pressure and as a result re-absorption of fluid would take place. At some point along the capillary there would be neither filtration nor re-absorption for at that point the two driving forces would be equal. Starling further suggested that, under normal conditions, there was a small excess of filtration over absorption and that this accounted for lymphatic flow.
It was thirty-one years later, in 1927, that Landis provided experimental evidence to support Starling's hypothesis. He occluded single capillaries of the frog mesentery with a fine glass rod under direct microscopic observation (Fig. 13.39).
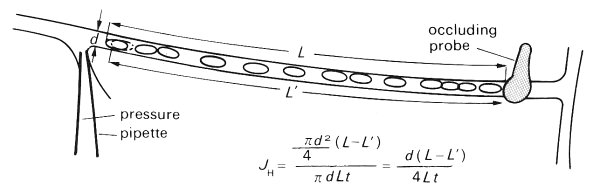
Fig. 13.39. The occlusion method for determining the filtration coefficient (/n). On occlusion the red cells can be seen to oscillate in time with the heart beat and slowly pack towards the probe. In time (the end red cell moves by L-L'. Vessel internal diameter is d.
When the capillary was occluded near to the venous end, the red cells upstream of the probe could be seen to oscillate in time with the heart beat and slowly pack towards the probe. When the occlusion was at the arterial end, the cells downstream of the probe could frequently be seen to move out of the vessel and into the venule. These observations were interpreted as evidence to support Starling's hypothesis since when the venous end of the capillary was occluded, the whole capillary was exposed to arteriolar pressure and filtration of plasma resulted. When the arterial end was occluded, the capillary was exposed to venular pressure and net absorption of interstitial fluid generally occurred. Landis assumed that the red cells fitted tightly in the capillary with no leak of plasma around the cell margin and that the capillary cross section was circular; then from measurement of the speed of movement of the red cells along the capillary he was able to make direct estimates of the filtration and absorption rates per unit area of capillary wall. These he related to the mean capillary hydrostatic pressure obtained by micropuncture of side branches of the vessel under observation. Results from his studies are presented in Fig. 13.40. The slope of the line through the data is the filtration coefficient JH (volume flow-rate, per unit time, area and pressure drop, see Chapter 9, §9.3); this was found to be approximately 5.6 x 10-5 (mm3 mm-2 s-1 N-1 m2.
In a further series of experiments in which the vessel wall was damaged by alcohol or anoxia or circulatory arrest, the slope of the line was considerably increased. However, the pressure at which there was no filtration or reabsorption (the intercept pressure) was unaltered. This pressure corresponds to the point where the hydrostatic pressure drop across the capillary wall just balances the colloid osmotic pressure difference. If in reality the tissue hydrostatic and colloid osmotic pressures are nearly zero, then the intercept pressure represents the mean value of the plasma colloid osmotic pressure.
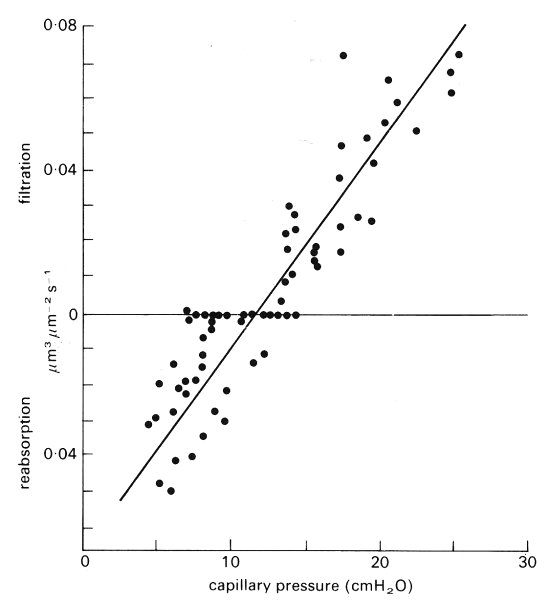
Fig. 13.40. The relation between fluid movement through the capillary wall and capillary pressure as measured in single capillaries of the frog mesentery. The slope of the line indicates the filtration coefficient of fluid filtered or re-absorbed. The intercept on the abscissa indicates the effective plasma colloid osmotic pressure. (From Landis (1927). 'Micro-injection studies of capillary permeability II: The relation between capillary pressure and the rate at which fluid passes through the walls of single capillaries'. Am. J. Physiol. 82, 233.)
The original technique of Landis has been modified to permit its application to mammalian capillaries whose diameters are less than those of the frog. Capillary filtration coefficients have now been measured in a number of tissues in different species; a few are listed in Table 13.3. In some cases venular filtration coefficients have also been measured and it can be seen that they are greater than in the feeding capillaries. It has further been observed, in both skeletal muscle and the mesentery, that filtration out of the plasma occurs throughout the length of the capillary and in the case of the cat mesentery may even do so in venules as large as 20-30 mm in diameter. The balance point between filtration and re-absorption is thus not necessarily in the mid-capillary region but may be within the venule. It may even be non-existent in the mesentery with no re-absorption taking place, all the plasma filtrate being removed via the lymphatics.
Table 13.3 Capillary filtration coefficients |
|
| Tissue | Coefficient (mm3 mm-2 s-1 N-1 m2) |
| Single capillaries | |
| Frog mesentery |
4 - 16 x 10-5 |
| Rabbit omentum:
arterial end venous end |
|
| Rat cremaster muscle |
1 x 10-5 |
|
Cat mesentery*
|
|
|
Capillary beds |
|
|
Human forearm |
1 x 10-6 |
|
Dog hind limb |
2.5 x 10-6 |
|
Cat hind limb |
3.5 - 5.2 x 10-6 |
|
Rabbit heart |
8.6 x 10-6 |
|
Dog lung |
0.22 x 10-6 |
Note that the data for capillary beds have been calculated assuming figures
for the capillary surface area per unit weight of tissue. Data reproduced from
Michel (1972). 'Flows across the capillary wall', In: Cardiovascular fluid
dynamics (ed. Bergel), vol. II. Academic Press, London. |
|
The observation that the filtration coefficient varies along the length of the microvascular bed means that the simple form of Starling's hypothesis cannot be used to model the behaviour of the whole exchange bed. The balance point may however be computed from Equation (13.3), for at that point
pc = (Pp - Pt) + pt
The plasma colloid osmotic pressure is approximately 3.0 x l03 N m-2 (30 cm H2O) and the sum of tissue hydrostatic and colloid osmotic pressures was shown earlier (§13.4.3) to be about - 0.5 x 103 N m-2 (- 5 cm H2O). Thus at the balance point, capillary hydrostatic pressure would be about 2.5 x 103 N m-2 (25 cm H2O). This is less than typical values for capillary pressures reported earlier (§13.4.1) but is representative of pressures to be expected within the venules.
The effect of changes in capillary hydrostatic pressure on capillary filtration and re-absorption can be seen in Fig. 13.41.
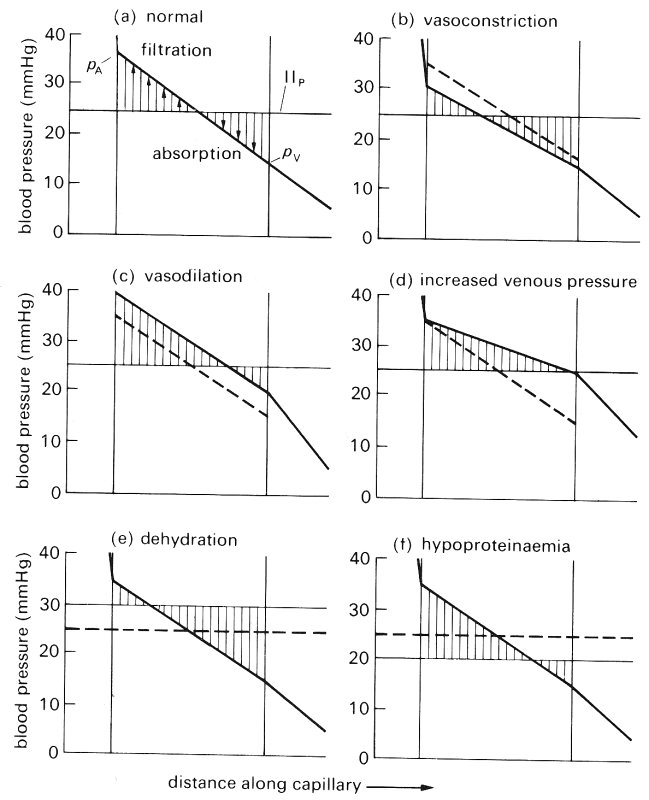
Fig. 13.41. Variations in filtration and absorption produced by changes in arterial and venous pressures, resistance and plasma colloid osmotic pressure, pA and pV are the pressures at the arterial and venous ends of the capillary and Pp represents plasma colloid osmotic pressure. The broken lines represent normal values taken from panel (a). (From Friedman (1971). 'Microcirculation'. In: Physiology (ed. Selkurt), pp. 259-273. Little Brown & Co., Boston.)
In (a) the normal situation can be seen. The effect of vasoconstriction (b) is to decrease the capillary pressure; as a result filtration is reduced and re-absorption from the interstitial space is enhanced. Vasodilatation (c) has the reverse effect. The effect of elevating venous pressure is to increase the capillary pressure, which favours filtration out of the capillary. The effects of dehydration (effective increase of plasma colloid osmotic pressure) and hypoproteinaemia (a reduction in plasma colloid osmotic pressure) are shown in (e) and (f) respectively.
13.7.2 Capillary pressure and filtration of water in whole organ preparations. The Landis occlusion technique can be used only for the study of single capillaries in flat beds such as the mesentery and cremaster muscle; alternative methods are required for beds such as limb muscles and organs. To study such beds, the isogravimetric technique has been developed; in this, the isolated organ or limb is perfused and weighed continuously. Under steady state conditions, the preparation is of a constant weight - the isogravimetric state. There is no net exchange of fluid between blood and tissue. If the blood flow-rate is varied it is found that the weight of the preparation tends to change, but that such alterations can be prevented by adjustment of central venous pressure (pv).
Assuming that the resistance to blood flow Rv between the capillaries and central veins is independent of blood flow-rate Q then the capillary pressure pc is given by
pc = pv + RvQ (13.4)
By plotting the blood flow-rate under isogravimetric conditions for various central venous pressures, an estimate may be made of pc from the intercept for venous pressure at zero flow-rate (Fig. 13.42).
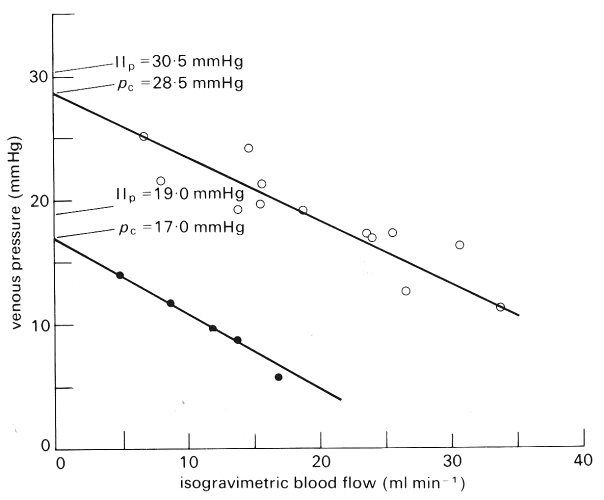
Fig. 13.42. The relation between blood flow-rate and venous pressure in the isolated perfused hind limb of the cat. The two sets of data were obtained for different plasma colloid osmotic pressures. (From Pappenheimer and Soto-Rivera (1948). 'Effective osmotic pressure of the plasma proteins and other quantities associated with the capillary circulation in the hind limb of cats and dogs'. Am. J.Physiol.152, 479.)
The linearity of the relation between pressure and flow shown in the figure supports the assumption of a constant post capillary resistance (Rv). Data for two experiments using plasma of differing colloid osmotic pressures are shown and the close correspondence between the estimated mean capillary pressure (pc) and the plasma oncotic pressure (Pp), which is predicted by the Starling hypothesis, can be seen.
The isogravimetric technique may also be used to obtain an estimate of the capillary filtration rate for a whole organ bed. Elevation of venous pressure with a constant blood flow-rate results in a sudden rise in the weight of the preparation followed by a continued but slower weight gain. The initial rapid increase is considered to result from the filling of the venous capacitance vessels whilst the slow continuing rise in weight is due to net filtration into the tissues. The rate of filtration per unit weight of tissue is found to be linearly proportional to the increase in capillary pressure above the isogravimetric value calculated on the basis of Equation (13.4). The slope of the line is the filtration rate per unit weight of organ per unit pressure difference - this is not the filtration coefficient as no estimate of the area over which filtration occurs has been made.
Table 13.4. Capillary filtration rates related to
|
||
|
Tissue |
Capillary type |
Filtration rate
|
| Cat hind limb | Continuous | 18 x 10-4 |
| Rat hind limb | Continuous | 40 x 10-4 |
| Rabbit heart | Continuous | 30 x 10-4 |
| Dog lung | Continuous | 2 x 10-4 |
| Cat intestine | Fenestrated | 2 x 10-4 |
| Cat kidney | Fenestrated | 20 x 10-4 |
|
Data derived from sources given in Altman and Dittmer (ed.) (1971). Biological handbooks, 'Circulation and respiration', pp. 502-3. Federation of American Societies of Experimental Biology. |
||
Measurements of the filtration rate have been made in a number of tissues and a few measurements are given in Table 13.4. It can be seen that filtration occurs far more readily through fenestrated endothelium such as is present in the intestine than through the continuous endothelial wall of skeletal muscle capillaries, even though the density of capillaries per unit weight of intestine is less than that in muscle. In practice the capillary filtration coefficient for a particular preparation may be calculated if the capillary surface area per unit mass of tissue is known; filtration coefficients for a number of tissue beds have been estimated, some of which are shown in Table 13.3. The filtration coefficients thus obtained are always considerably less than those obtained more directly on single capillaries. However, this is perhaps not too surprising as morphometric studies of capillary surface area obtained post-mortem give a poor indication of the number of capillaries open and functioning under more physiological conditions. Any overestimate of capillary surface area will lead to an underestimate of the filtration coefficient. Furthermore, measurements on single capillaries involve surgical exposure, cannulation, and thermal effects from microscope stage lighting, all of which may increase permeability.
13.7.3 The dependence of plasma oncotic pressure on protein concentration. As can be seen from Equation (13.3), the rate of filtration of water out of the plasma depends upon the values of both hydrostatic and osmotic pressures in the plasma and tissue space. As water and small molecules are filtered out of the plasma, the protein concentration increases; the resultant increase in plasma concentration (g per 100 ml) oncotic pressure should be predictable by application of van't Hoff's law (Equation (9.14), §9.7), which relates osmotic pressure P to molar concentration c for dilute solutions:
P = cRT
where T is the absolute temperature and R the Universal Gas Constant. However, such predictions underestimate the actual increase in osmotic pressure; as the concentration of protein increases the osmotic pressure increases disproportionately. This effect can be seen from Fig. 13.43 in which the plasma oncotic pressure is plotted as a function of plasma protein concentration.
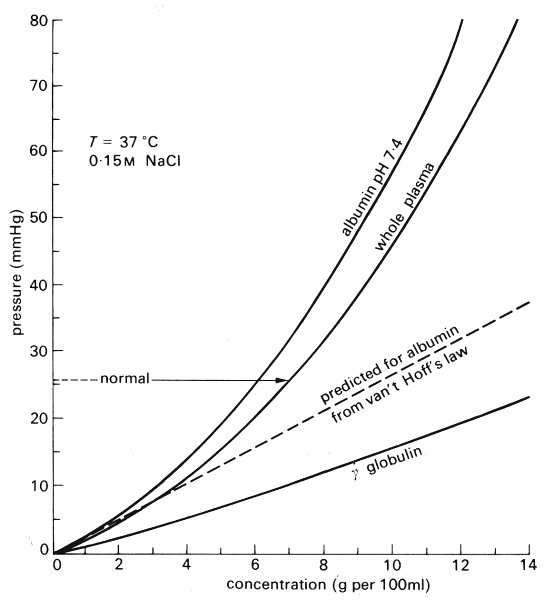
Fig. 13.43. The variation of osmotic pressure with concentration for whole plasma, albumin, and gamma-globulin. The dotted line indicates the predicted osmotic pressure for albumin based upon van't Hoff's law. (After Landis and Pappenheimer (1963). 'Exchange of substances through the capillary walls'. In: Handbook of physiology. Section 2: Circulation vol. II (ed. Hamilton and Dow), pp. 961-1034. American Physiological Society, Washington D.C.)
Also plotted is the osmotic pressure of an albumin solution as a function of concentration compared with that predicted on the basis of the van't Hoff relationship assuming dilute solutions. The cause of this behaviour is very complex, depending partly on the effects of the large molecules trapping water, and also on electrical charge effects on the molecules themselves.
13.7.4 Evidence for the existence of filtration pores in the capillary wall. The transport of water and water-soluble small molecules across the capillary wall for a given hydrostatic or osmotic pressure gradient is far greater than it is across the red cell membrane and it has long been postulated that such substances cross the wall via narrow pores. The suggestion that lipid-insoluble materials can only filter or diffuse through a very small fraction of the capillary wall is also highly suggestive of the existence of specialized water-filled pores or slits penetrating the endothelial lining of the vessels.
It was shown earlier (§13.2.5) that the cleft between endothelial cells is a long slit approximately 15-20 nm wide, except over a narrow zone where adjacent membranes almost fuse together. When the zone of fusion is intermittent (macula occludens), the oval slit or gap between adjacent sites of fusion is thought, from electron microscopic studies, to be approximately 8 nm wide. Thus this gap would provide the greatest restriction to filtration or diffusion along an intercell cleft. It was also pointed out that fenestrated capillaries may be so designed to provide a good diffusion path via the circular fenestrae and that discontinuous capillaries possessed very large intercell gaps which would clearly provide a very low transport resistance.
It is considered that the intercell cleft is in fact the predominant pathway for the filtration of water and small water-soluble molecules.
13.7.5 Diffusion across the capillary wall. The process of filtration and re-absorption can occur only through water-filled passages across the capillary wall. In principle, however, diffusion of molecules across the wall can take place across the membrane of the endothelial cells. Indeed it does seem to do so for highly lipid-soluble substances such as the respiratory gases; with such molecules it appears that the area available for diffusion is virtually the total surface area of the membrane.
Larger molecules and lipid-insoluble molecules, however, do not appear to be capable of diffusing across the endothelium with such facility. Nevertheless the capillary wall possesses a far higher permeability to such substances than does the red cell membrane and the wall also has a low but definite permeability to larger molecular weight molecules such as albumin.
It will be recalled that, in free dilute solution, the diffusional rate of transport Js of a substance may be described by Fick's law (§9.1):
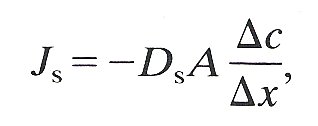 (13.5)
(13.5)
where Dc/Dx is the gradient of concentration of the substance in the direction of transport, A is the cross-sectional area across which transport occurs, and Ds is the diffusion coefficient. As was explained in §9.6, the above equation may be conveniently rewritten
Js = PsAmDc (13.6)
(where -Ps = Ds/Dx), because the exact distance over which the concentration of the substance is changing cannot really be determined. Am is the surface area of membrane and Ps is called the 'permeability coefficient' or simply 'permeability'.
Table 13.5 Permeabilities of skeletal muscle capillaries to lipid-insoluble molecules in skeletal muscle |
|||||
| Molecule | m.w. | Radius (nm) | P (x 10-6 cm s-1) |
D (x 10-6 cm2 s-1) |
P/D (x 10-3 cm-1) |
| H2O | 18 | 0.15 | 0.54 | 34 | 17.2 |
| Urea | 60 | 0.26 | 0.26 | 19.5 | 13.5 |
| Glucose | 180 | 0.37 | 0.090 | 9.0 | 10.0 |
| Sucrose | 342 | 0.48 | 0.050 | 7.0 | 6.9 |
| Raffinose | 504 | 0.57 | 0.039 | 6.4 | 6.0 |
| Inulin | 5500 | 1.30 | 0.005 | 2.5 | 2.6 |
| Myoglobin | 17 000 | 1.90 | 0.0004 | 1.7 | 0.3 |
| Serum albumin | 67 000 | 3.60 | < 10-5 | 0.85 | 0 |
|
Data derived from the following sources: |
|||||
Permeability coefficients have been obtained for a number of non lipid-soluble molecules in mammalian skeletal muscle; some of them are given in Table 13.5. It can be seen that as molecular weight and approximate molecular radius increase, the permeability decreases considerably. A decrease in permeability is to be expected because the diffusion coefficient decreases with increasing molecular weight; however, Table 13.5 shows that permeability falls relative to the diffusivity as molecular weight increases. This would suggest that the area available for diffusion decreases, or that the diffusion path length increases, or that the resistance to diffusion increases for some other reason. If the path length for diffusion is approximately the thickness of the endothelial cell and independent of molecular size, then the effective area for diffusion of lipid-insoluble materials is far less than the actual surface area of the capillary wall.
If the effective area of membrane available for transport of a particular solute is As, then Equation (13.6) should be rewritten as
Js = (PsAs)Dc
or
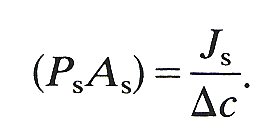 (13.7)
(13.7)
Most studies of permeability are in fact concerned with obtaining the product (PsAs) for different molecules from the experimentally derivable quantities Js and As. If the effective area of membrane available for the transport of two molecules of differing sizes is the same, then comparison of the value of (PsAs) gives a direct indication of the relative permeability; however, it is not always appropriate to make such an assumption, as will be discussed later.
13.7.6 Methods of measuring permeability coefficients. A number of methods have been developed to measure the permeability of the wall. All are very elegant but suffer from various experimental and computational difficulties; measured permeabilities for a given molecule in a particular tissue vary considerably according to the method used. There appear to be significant differences in the value obtained in different tissues, and whilst this may be due to genuine differences between the endothelial cell linings it is thought also to reflect the shortcomings of the various techniques.
In order to determine the permeability of a vessel, it is necessary to know not only the net solute flow between blood and tissue but also the concentration gradient across the wall. Because the blood is flowing through the capillary while transport is taking place, the concentration gradient and solute transport will vary with distance along the capillary. Since it is not possible to measure these quantities from point to point it is necessary to estimate an effective concentration gradient over the whole length of the vessel; in turn the choice of a suitable form of mean gradient depends upon the complexity of the model describing exchange between the blood and tissue.
It must also be appreciated that the blood flow-rate can independently have a significant effect on exchange in certain circumstances, and this should not be confused with an alteration in the permeability of the wall. Consider the situation where an exchangeable molecule is injected into the arterial blood approaching a capillary. As the blood passes through the capillary the concentration of the marker molecule will fall progressively from the arterial to venous end, as shown in Fig. 13.44.
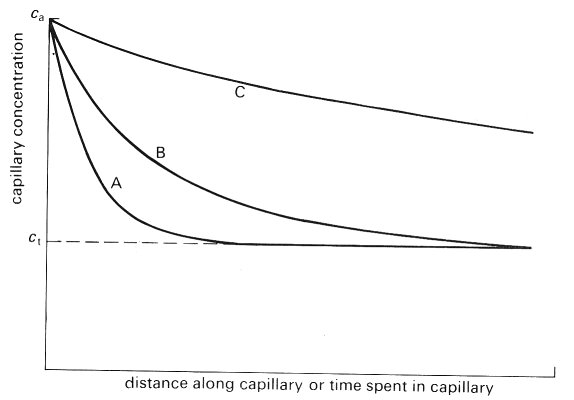
Fig. 13.44. The fall in blood concentration of three substances as they exchange with the tissues during flow through the capillary. The capillary wall is most permeable to substance A and least to C. In the case of A and B, equilibrium between blood and tissues is achieved before the blood leaves the capillary and conditions are 'flow limited'. C is not equilibrated and exchange is said to be 'diffusion limited'. (From Michel (1972). 'Flow across the capillary wall'. In: Cardiovascular fluid dynamics (ed. Bergel), vol. II. Academic Press, London.)
If the wall is highly permeable to the marker but has a low capacity, the concentration will initially fall rapidly (curve A) and then, when equilibrium is achieved, the concentration will fall no farther with distance along the capillary. Curve B represents the situation where the molecule achieves equilibrium with the tissue just at the end of the capillary. Curve C illustrates the situation where the capillary is not long enough to allow the marker to equilibrate between blood and tissue. It can be seen that, since the rate of solute uptake is the product of the blood flow-rate and the arterio-venous concentration difference (ca - cv), the uptake in situations A and B is the same, but is less for C.
If the blood flow-rate were reduced, the rate of uptake would be reduced in cases A and B in direct proportion to the degree of decrease in blood flow. The uptake of C would also be reduced but to a much lesser degree, since the increased residence time in the blood would allow a greater time for exchange and an increase in the arterio-venous difference. An increase in the blood flow-rate, whilst increasing the rate of uptake in all situations, will have most effect in case A and least in case C. These differences in the dependence of uptake on blood flow-rate have led to the terms 'flow limited' and 'diffusion limited' uptake. Because uptake in cases A and B can be increased only by increasing flow-rate they are described as flow limited In case C, because diffusion equilibrium is not achieved, conditions are said to be diffusion limited.
When carrying out studies of permeability it is essential to do so at various flow-rates in order to ensure that the solute being investigated is not flow limited. In both A and B the arterio-venous concentration difference is the same and any calculation of the effective concentration gradient across the wall based on the arterio-venous difference in concentration would yield the same permeability in the two cases. Clearly the wall is more permeable in case A than case B.
The uncertainties associated with flow limitation have meant that most studies of permeability have been on lipid-insoluble molecules, and it has not been possible to obtain values of the permeability for small highly fat soluble molecules.
The introduction of radioactively labelled isotopes to physiology provided the opportunity to use the extremely elegant technique of indicator dilution for measuring the product of permeability and effective area. A radioactive isotope of a molecule known to remain in the blood and a differently labelled isotope of a molecule capable of traversing the capillary wall are injected together as a bolus into a small artery. Samples are taken from a vein draining the capillary bed. The relative concentration of the isotopes in the venous samples compared with the relative values when injected indicates the fraction of the exchangeable marker which has crossed the wall. Fig. 13.45 shows the results of an experiment on the permeability of sucrose, in which albumin was used as the non-exchanging intravascular marker.
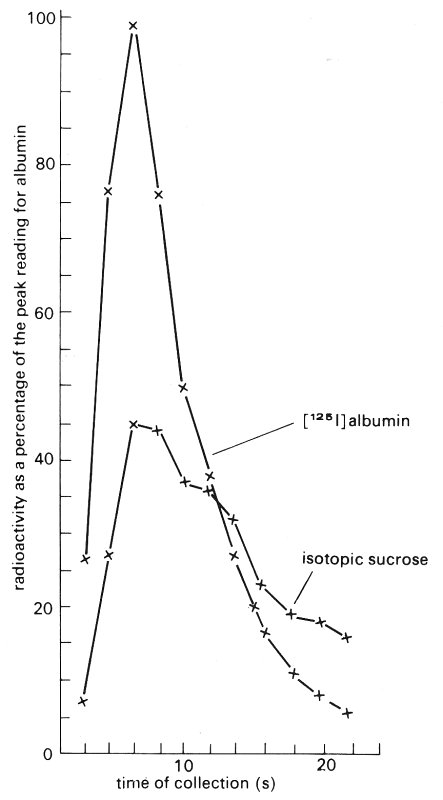
Fig. 13.45. The relative concentrations of radio-actively labelled albumin and sucrose as monitored in a vein after simultaneous injection in an artery.
The sucrose concentration rises more slowly and to a lower peak than the albumin because of its extraction into the extravascular space. At some time after the peak concentrations have been reached, the curves cross. This is because the albumin has been largely washed out of the capillary system but the venous sucrose concentration is maintained relatively high by transport back from the tissues where the sugar concentration has become higher than the falling blood concentration.
If it is assumed that initially the transport out of the capillary at any point is proportional to the local concentration in the blood (the tissue concentration of labelled sucrose is initially zero), then the blood concentration of sucrose will fall exponentially along the capillary. It can then be shown that the mean capillary concentration c is given by
c = (ca - cv)/ln(ca/cv)
where ca and cv are the sucrose concentrations at the arterial and venous ends of the bed. These concentrations may be obtained directly from the heights of the peaks of the curves in Fig. 13.45; the height of the albumin peak gives the arterial concentration of sucrose and the sucrose peak gives the venous sucrose concentration. Because the initial tissue concentration of the sucrose isotope is zero, the mean concentration difference across the vessel walls is equal to c. Also the rate of uptake of sucrose is given by
Js = Q (ca - cv)
where Q is the blood flow-rate through the capillary bed. Thus substitution into Equation (13.7) gives
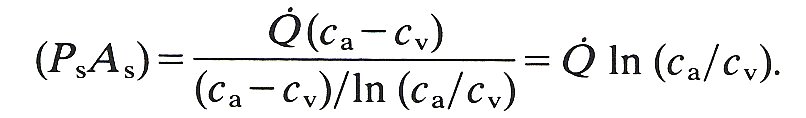
Great advantages of the indicator dilution technique are that it may be carried out on an intact circulation, and is relatively easy to perform experimentally. However, the method does involve an important assumption. It is assumed that all vessels in the bed have the same permeability and the same ratio of exchange surface area to blood flow. Any visual study of a functioning capillary bed makes such an assumption seem dubious. Any such non-uniformity in the bed will lead to an underestimate of the permeability. In order to overcome this problem the permeability is measured at as high a flow-rate as possible. It is also assumed that the two molecules studied are distributed identically within the capillary bed. Whilst this might at first seem probable, it is not necessarily the case. The dispersion of the molecules within the flowing blood depends to some extent upon the molecular diffusivity, and since the molecules differ in size it is to be expected that there will be some difference in their distribution in the vasculature because of the effects of Taylor dispersion as discussed in Chapter 12 (§12.9.1).
In another approach to the determination of permeability, the plasma and lymph concentrations of a given molecule are compared. It was pointed out earlier in the chapter that, under steady state conditions, while the greater part of the water and small molecules which pass out of the blood at the arterial end of the capillary is returned at the venous end, the remainder leaves the interstitial space via the lymphatic drainage system. Plasma and lymph electrolyte concentrations are very similar, but their protein concentrations are not, being higher in the plasma than in the lymph; furthermore the relative concentrations of the various proteins themselves are different, as shown in Table 13.6. Globulin, a molecule rather larger than albumin, appears to be less capable of crossing the capillary wall of some organs than others.
Table 13.6. Total protein and albumin: globulin ratios in plasma and lymph from various sources |
||
| Total protein (g per 100 cm3) |
Albumin:globulin ratio |
|
| Plasma | 6.3 | 1.43 |
| Thoracic duct lymph | 4.0 | 1.50 |
| Muscle lymph | 2.3 | 1.54 |
| Intestinal lymph | 3.8 | 1.50 |
| Liver lymph | 5.3 | 1.48 |
|
Data derived from Courtice (1972). "The chemistry of lymph'. In: Lymph vessel system (ed. Meessen). Springer Verlag, Berlin and Heidelberg. |
||
Molecules of known molecular size are introduced into the circulation intravenously, and the plasma and lymph concentration is monitored. (Direct measurement of the concentration of the marker molecule has been attempted in the interstitial space when radioactive molecules have been used.) When steady state conditions are achieved, the net flow-rate of the solute through the capillary walls is equal to the flow-rate of the solute in the lymphatic channels. The flow of the molecule out of the capillaries will be by both filtration and diffusion. However, when the permeability of relatively large molecules is being studied, the lymph concentration (cL) is found to be much less than the plasma concentration. Thus it is reasonable to assume that the net filtration is very small because the resistance to the molecules within the pores is very high, and transport is mainly by diffusion. Then
JLcL = (PsAs)(cp - cL)
where JL is the lymphatic flow-rate, cp is the plasma concentration of the molecule and PsAs is the permeability area product for the molecule as defined in Equation (13.7). The effective concentration difference across the capillary wall as given by (cp - cL) is based first on the fact that the net exchange rate is very low and the arterio-venous fall in concentration is very small compared with the absolute level, and secondly on the assumption that the diffusion resistance is all at the capillary wall and interstitial fluid concentrations are the same as the lymphatic concentration.
The permeability of the wall to a number of substances has been measured in this way, in particular polysaccharides such as dextrans, with a range of molecular weights, and the polymer polyvinyl pyrrolidone (PVP), whose molecular weight ranges from 10,000 to over 200,000. The variation in the permeability area product with molecular weight is found to vary as shown in Fig. 13.46.
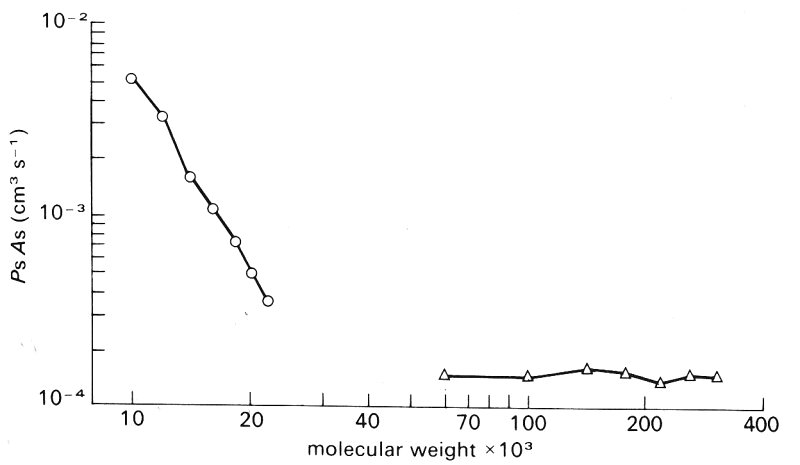
Fig. 13.46. Capillary permeability area product as obtained from plasma: lymph ratios and lymph flow-rate for PVP molecules of a range of sizes. Note that permeability falls with increasing molecular weight in the low weight region but becomes constant at high molecular weights. (From Renkin (1964). Transport of large molecules across capillary walls'. Physiologist 7, 20.)
In the lower molecular weight range the permeability falls with increasing molecular weight, but in the higher molecular weight range permeability becomes independent of molecular size. This would suggest that large and small molecules cross the capillary membrane by a different mechanism.
We now examine the three basic assumptions which underlie the principle of this method of obtaining the capillary permeability, (i) The bulk flow filtration term is assumed to be negligible; in practice this appears to be acceptable as the permeability is only slightly increased when lymph flow is elevated, (ii) The concentration gradient between the outside of the capillary wall and the lymphatic capillaries is assumed to be negligible. Whilst a small gradient may exist for larger molecules, it is thought to be negligible for smaller ones so that the assumption is probably reasonable, (iii) The third assumption is that the lymphatic concentration is representative of the interstitial fluid concentration; this is rather questionable. If there is a range of permeabilities among the capillaries in a region then the lymph will be predominantly composed of the water and molecules from those capillaries which are most permeable, and the local interstitial fluid will be relatively high in protein concentration. Thus there will be a spectrum of interstitial fluid compositions, and the regional lymph composition will represent a mean of the ultrafiltrates of all capillaries.
One of the earliest methods of determining permeability used the isolated hind limb preparation. The solute molecules were added to the perfusate flowing to the capillary bed; this caused water to be drawn out of the limb tissue into the plasma. To prevent this, capillary pressure was raised by increasing venous pressure until the limb regained and maintained its original weight. The amount by which the capillary pressure was raised equalled the osmotic pressure difference across the capillary walls resulting from the introduction of the solute. The transport rate Js of the test solute across the wall was estimated from the product of the arterio-venous concentration difference and the blood perfusion rate. The effective concentration difference across the wall was estimated from the osmotic pressure change (DP) using van't Hoff's law (Equation (9.14)). Then on substituting into Equation (13.7), one obtains
PsAs = Js (DP/RT)
Whilst this technique appears very attractive, its major drawback lies in the assumption that the effective concentration difference across the wall can be computed simply from van't Hoff's law. In fact the law breaks down for many large molecules at all but the most dilute concentrations (see §13.7.3). Furthermore, the law assumes that the membrane acts as a perfect semi-permeable barrier and that all the solute molecules are prevented from crossing; the fact that the membrane is restricting but not prohibiting solute transfer leads to a reduced osmotic pressure (see Chapter 9, §9.7).
The size of the osmotic reflection coefficient or (Equation (9.16)) depends upon hydrodynamic as well as diffusional factors influencing the motion of molecules within the membrane passages, and currently no satisfactory theory predicting its magnitude is available. The estimation of this coefficient is one of the most important areas of membrane physics of today.
The value of s is believed to depend upon the relative size of the restricted diffusion coefficients of the solute (Ds') and solvent (Dw'), thus
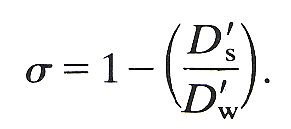 (13.8)
(13.8)
The effective diffusion coefficient under these circumstances may be given by
D' = DAs/Ap (13.9)
where D is the free diffusion coefficient and As and Ap are the apparent and true areas for diffusion. Thus combining Equations (13.8) and (13.9) we obtain
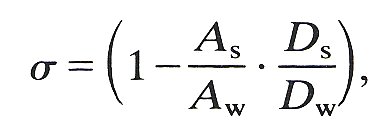
where As and Aw, are the apparent areas for diffusion of solute and solvent respectively, assuming that the true areas available for diffusion of solute and solvent are in fact the same. In fact it is now thought that the area of membrane available for the transport of water and most lipid-insoluble molecules is probably not the same and thus Equation (13.10) is a poor description of the osmotic reflection coefficient.
13.7.7 The diffusion pathway across the capillary wall. Two general types of study have been conducted to try to elucidate the diffusion pathway across the capillary wall. In the first, lipid-insoluble molecules of known molecular size, capable of detection by electron microscopy, were introduced into the capillary lumen and allowed to diffuse out through the capillary wall. The tissue was then fixed and prepared for microscopy, and their location and concentration in the wall and interstitial space studied. In the second approach, the permeability studies reported above have been used to predict theoretically the existence of pores of a certain size and then to relate the pore size to structures in the wall that are identifiable with an electron microscope.
In continuous capillaries, it has been shown that molecules of intermediate size (horse-radish peroxidase, m.w. about 40,000) enter the extravascular space beyond the endothelium via the vesicles and are not extensively observed within the intercell clefts. Smaller molecules (cytochrome peroxidase, m.w. about 12,000) were observed to move out of the capillaries more rapidly and could be observed in the intercell clefts in concentrations diminishing with distance from the luminal surface. On the basis of these and similar studies it has been suggested that the intercell cleft is capable of allowing the passage of relatively small molecules, but inhibits the transport of large molecules.
These studies are compatible with the observed dependence of permeability on molecular weight as shown in Fig. 13.46. At the high molecular weight end permeability is largely independent of molecular size; the size at which this happens is in the region of 40,000.
13.7.8 The Pappenheimer Equivalent Pore Theory. Throughout this chapter it has been strongly suggested that the filtration and diffusion across the capillary wall occur via pores. This suggestion has long been proposed, but it was in 1951 that Pappenheimer and his colleagues proposed a quantitative model for the diffusion of molecules through pores of dimensions comparable with their size. The theory provides a very convenient description of flow across a membrane and is capable of making very precise predictions about the structure of the membrane.
The theory of Pappenheimer gives an estimate of the restricted diffusion coefficient compared with the free diffusion coefficient in terms of the apparent and true pore areas as defined in Equation (13.9). It suggests that the effective diffusion coefficient is reduced because the effective pore area is diminished as the result of hindrance at the entrance to the pore due to shape differences, and that the increased hydrodynamic drag on a molecule passing through a confined space, compared with that in an unbounded medium, causes a diminution in the diffusion coefficient.
Thus for a molecule of radius a to enter a pore of radius r without touching its sides, the true target area As is p(r-a)2 or
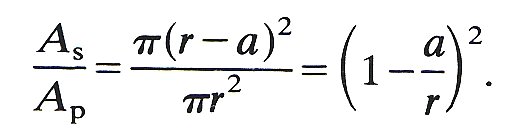 (13.11)
(13.11)
The amount by which the drag on a molecule is increased in a narrow pore is very hard to assess as it will depend not only upon the relative dimensions but upon the shape of the molecule, the charge distribution on its surface, its flexibility and many other factors. Some of these effects (e.g. shape and flexibility) are partially allowed for when defining the molecular radius on the basis of its Stokes-Einstein equivalent (Equation (9.6)). If the frictional resistance in free motion is f and that when passing through a pore is fR then a good approximation of the effect has been found to be:
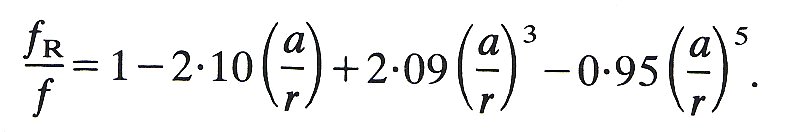 (13.12)
(13.12)
On the basis of the Nernst equation (Equation (9.4), §9.1),
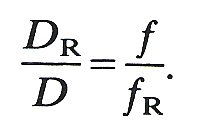 (13.13)
(13.13)
Substituting for Equations (13.11), (13.12), and (13.13) in Equation (13.5)
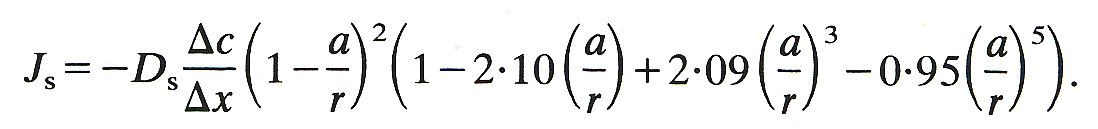 (13.14)
(13.14)
Thus if the permeability area product (Equation (13.7)) is measured in a given preparation for a range of molecular sizes, it is possible (using Equation (13.14)) to obtain an estimate of the equivalent size of the pores through which diffusion takes place. Comparison of the pore theory with experimental data obtained in the hind limb preparation is shown in Fig. 13.47. It can be seen that as molecular size is increased the permeability falls in a manner very close to that predicted from Equation (13.14), assuming the pores to be circular and of 4 nm radius.
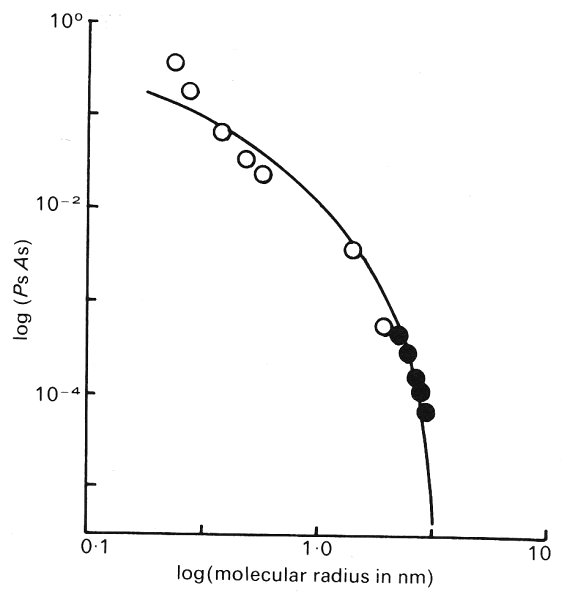
Fig. 13.47. The permeability of cat and dog hind limbs to molecules of different molecular radius. The curve is that predicted on the basis of restricted diffusion through pores of 4 nm radius. (From Michel (1972). 'Flow across the capillary wall'. In: Cardiovascular fluid dynamics (ed. Bergel), vol. II, Academic Press, London.)
Such agreement between experiment and theory is very attractive, particularly when electron microscopic studies of the intercell cleft indicate that the gap is of this order of size. However, such close agreement is not always obtained and many further studies are needed to draw firmer conclusions about the structure of the diffusion pathway in a wide range of tissues.
13.7.9 The pathway for water transport across the capillary wall. Using the Pappenheimer pore theory it is also possible to obtain an estimate of the size of the pores in the capillary walls from a knowledge of the water filtration rate. If the pores are of the order of 4 nm in radius, they are considerably larger than the radius of the water molecule and it is therefore reasonable to assume that the water flow may be described using Poiseuille's law (Equation (5.1), §5.1); evidence based on water transport through artificial membranes with pores of such a size supports this assumption. If the filtration rate is JH for an effective filtration driving force of (Dp - DP) (Equation (13.3)), then
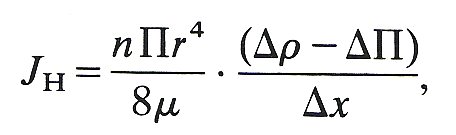
where n is the number of pores of radius r in the membrane whose thickness is Dx. If the pore area available for water transport is Aw then
Aw = n P r2
and
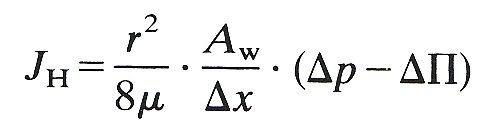
or
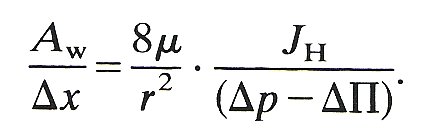 (13.15)
(13.15)
Thus we may obtain the pore area per unit path length for water if we already know the pore radius from measurements of the filtration coefficient as obtained in §13.7.2 using the isogravimetric preparation. It is also possible to obtain the effective pore area per unit path length (As/Dx) for the diffusion of molecules of various radii using the same preparation:
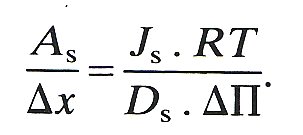 (13.16)
(13.16)
If we assume that the pore area Aw, available for water transport is the true pore area Ap for solute diffusion, then dividing Equation (13.15) by Equation (13.16) and equating the result with Equation (13.14) provides an explicit equation for pore radius in terms of experimentally derivable quantities. Solution of this equation gives an effective pore radius of 14 nm, which is considerably larger than the value obtained by other methods and the discrepancy cannot be reconciled on the basis of the inaccuracies associated with the experiments.
However, the discrepancy can be accounted for if it is not assumed that water is constrained to pass only through the pores available to lipid-insoluble molecules. If the pores are taken to be 4 nm radius then it can be calculated that only half the water passes through the pores available to the solute, the remainder using other pathways through the wall.
13.7.10 The transport of large molecules. For a long time it was believed that the capillary wall was impermeable to molecules larger than those of albumin. However, studies such as those in Fig. 13.46 have shown that the wall has a very low but definite permeability to large molecules and that it is virtually independent of molecular size. There have been a number of electron microscope studies aimed at identifying large pores in the capillary wall capable of allowing the passage of such molecules; the fenestrae in some capillary walls may provide such a pathway. The cytoplasmic vesicles present in all capillary walls are also considered to be responsible for the transport of the large molecules. Experimental studies have shown that plastic microspheres of diameter less than about 30-70 nm are capable of crossing the hind limb capillary walls.
If the transport of such large molecules and particles is via large pores then we would expect the permeability to vary in proportion to the molecular diffusivity. Studies in the hepatic and intestinal beds with Dextran molecules, whose diffusivity decreases with the square root of molecular weight, have shown a consistent linear decrease in permeability with the square root of molecular weight; indeed these are fenestrated capillary systems. Similar studies carried out on skeletal muscle beds, which contain continuous endothelium, do not show such a clear relation. It is possible that permeability is much less dependent upon molecular diffusivity and that transport is via the vesicles rather than unidentified pores.
It was Palade in 1953 who first proposed that the vesicles acted as a transport system across the endothelium and since that time some effort has been devoted to assessing their importance and elucidating the mechanism. As was explained earlier, the membrane bounding vesicles is, as far as can be determined, the same as the membrane bounding the cell and vesicles can be found either free within the cytoplasm of the cell or attached to the cell wall. Because of their small size, their behaviour is extremely difficult to study and great reliance must be placed on the use of the electron microscope.
Three important processes associated with the vesicles have been identified. These are the movement of vesicles within the body of the cell, their attachment and detachment at the cell surfaces, and the exchange of their contents with either the blood or interstitial fluid.
The movement of vesicles within the cell is thought to occur through Brownian motion as a result of collisions with the constituent molecules of the cytoplasm. However, it is hard to predict the effective diffusivity of the vesicles, even if their density is assumed to be the same as that of the cell, because the effective viscosity of cytoplasm is unknown. Furthermore the long range vesicle displacements cannot be the same as in an unbounded medium; the gap between opposing cell walls is in the region of only 0.3-0.4 mm or 4-5 vesicle diameters (approximately 70 nm). It is however possible to predict (using elementary kinetic theory) that the impact of surrounding molecules could rapidly accelerate a vesicle to a velocity of about 30 cm s-1. The viscous drag on such a small particle is very large and as a result it will be brought back to rest in a small fraction of a second.
The processes associated with attachment and detachment of vesicles to and from the cell wall are even less well understood. If a vesicle moving around in the body of the cell comes sufficiently close to the wall (say a distance of 2-3 nm), then it enters a region in which the Van der Waals' attraction force will pull it towards the wall. For this to happen the cytoplasm must be squeezed out of the gap between the vesicle and the wall; as the gap narrows the force required to exclude the fluid increases, but so does the Van der Waals' force. When the vesicle approaches very close to the wall, the latter becomes distorted, as shown in Fig. 13.48.
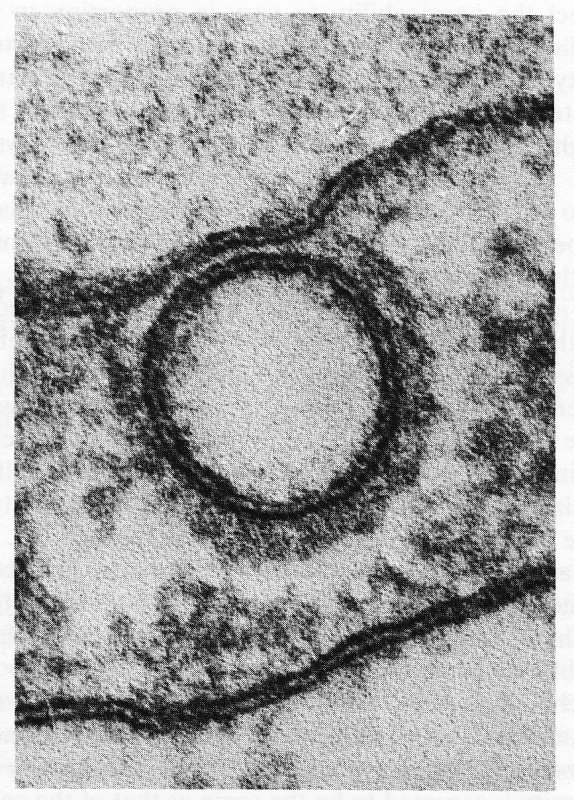
Fig. 13.48. The close approach of a vesicle to the endothelial cell surface showing the deflection of the surface of the cell membrane. (From Palade and Bruns (1968). 'Structural modulations of plasmalemmal vesicles'. J. Cell. Biol. 37, 633-49.)
The two membranes then fuse to form a diaphragm, which finally splits to give the vesicle an opening to the external environment of the cell (Fig. 13.49).
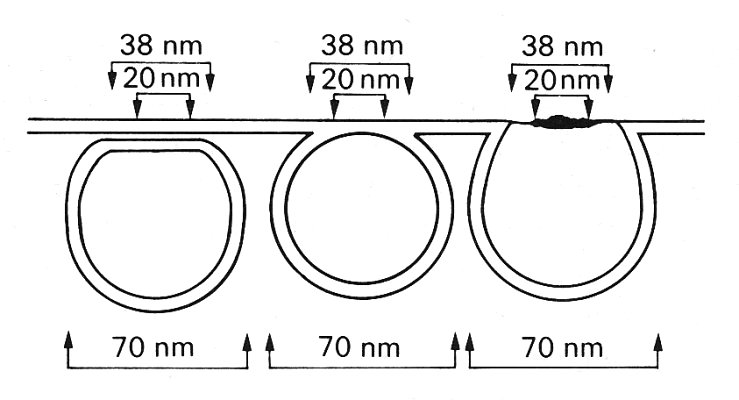
Fig. 13.49. Schematic illustration of the progressive fusion and rupture of the membrane between a vesicle and the cell wall. (From Palade and Bruns (1968). 'Structural modulations of plasmalemmal vesicles'. J. Cell. Biol. 37, 633-49.)
The remnants of the diaphragm can be clearly seen in Fig. 13.50.
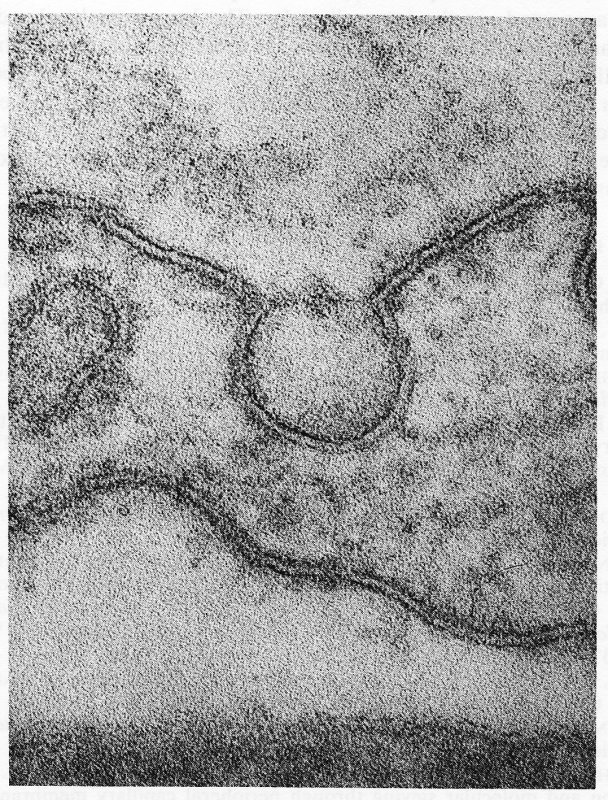
Fig. 13.50. A vesicle shortly after the diaphragm across the surface has shattered. The central knob of the diaphragm can be clearly seen. (From Palade and Bruns (1968). 'Structural modulations of plasmalemmal vesicles'. J. Cell. Biol. 37, 633-49.)
The mechanism of detachment is obscure; however, once it has occurred the vesicle is again free to move under the influence of Brownian motion. It can either be attracted back to the wall and re-attach at or near the original point, or move to some remote site possibly on the opposite wall. The typical lengths of time a vesicle spends free within a cell or attached at a wall have been estimated very tentatively to be about 5 s and 3 s respectively.
The loading and unloading of the contents of a vesicle take place by diffusion. Thus the vesicles provide a pathway for the transport of water and small molecule weight materials as well as large molecules. However, because of the relative slowness of this pathway, it is unimportant for molecules capable of being transported via the intercell clefts. The largest molecules capable of being transported by the vesicle system are those just able to pass through the neck of the vesicle, that is, lipoproteins of molecular diameters of about 50 nm diameter. Somewhat smaller molecules will enter the vesicle but experience restricted diffusion passing through the neck. The permeability of the wall to molecules transported via the vesicles thus may depend to some extent upon the diffusion coefficient of the species.
CRONE, C. and LASSEN, N. A. (1970) (ed.). Capillary permeability. Munksgaard, Copenhagen.
FUNG, Y. C. (1968). Biomechanics, its scope, history, and some problems of continuum mechanics in physiology. Appl. Mechan. Rev. 21, 1-20.
GAEHTGENS, P. and UEKERMANN, U. (1971). The distensibility of venous microvessels. Pflug. Arch. ges. Physiol. 330, 206-16.
LANDIS, E. M. and PAPPENHEIMER, J. R. (1963). Exchange of substances through the capillary walls. In: Handbook of physiology. Section 2: 'Circulation', Vol. II (ed. W. F. Hamilton and P. Dow), pp. 961-1034. American Physiological Society, Washington, D.C.
LIGHTFOOT, E. N. (1974). Transport phenomena and living systems. Wiley-Interscience, London.
JOHNSON, P. C. (1973). The microcirculation and local humoral control of the circulation. In: Cardiovascular physiology (ed. A. C. Guyton). M.P.T., London.
MAJNO, G. (1965). 'Ultrastructure of the vascular membrane'. In: Handbook of physiology (ed. W. R. Hamilton and P. Dow), Section 2: 'Circulation', Vol. II, pp. 2293-375. American Physiological Society, Washington, D.C.
MICHEL, C. C. (1972). 'Flows across the capillary wall'. Cardiovascular fluid dynamics, Vol. II (ed. D. H. Bergel), Chapter 17. Academic Press, New York.
MIDDLEMAN, S. (1972). Transport phenomena in the cardiovascular system. Wiley- Interscience, London.
PAPPENHEIMER, J. R., RENKIN, E. M., and BORRERO, L. M. (1951). Filtration, diffusion and molecular sieving through peripheral capillary membranes. Am. J. Physiol. 167, 13-46.
SNASHALL, P. D., LUCAS, J., Guz, A., and FLOYER, M. A. (1971). Measurements of interstitial 'fluid' pressure by means of a cotton wick in man and animals: an analysis of the origin of the pressure. Clin. Sci. 41, 35-53.
WEINBAUM, S. and CARO, C. G. (1976). A macromolecule transport model for the arterial wall and endothelium. J. Fluid. Mech. 74, 611-40.
WOLSTENHOLME, G. E. W. (1969) (ed.). Circulatory and respiratory mass transport. Churchill, London.
ZWEIFACH, B. W. (1974). Quantitative studies of microcirculatory structure and function. Circulation Res. 34, 834-66.