This chapter is concerned with the mechanical properties of the blood and its constituents. We shall examine in later chapters (12 and 13) the flow of blood in blood vessels and its contact with their walls. The mechanics of fluids, discussed in Chapters 4 and 5, provide a background to the material that follows.
Blood is a suspension of the formed elements (the various blood cells) and some liquid particles (the chylomicrons) in the plasma. Plasma itself is an aqueous solution containing numerous low molecular weight organic and inorganic materials in low concentration, and about 7 per cent by weight of protein (Table 10.1). The mechanical property of blood which is of principal interest to us is its viscosity. In order to understand what determines the viscosity of whole blood we must first consider what governs the viscosity of simple fluids and suspensions, then the mechanical properties of the plasma (§10.1.3) and the suspended elements (§10.3.1), and finally whole blood (§10.6.)
Table 10.1 Outline of composition of plasma |
|||
|---|---|---|---|
|
Material
|
Concentration
(g per 100 ml) |
Molecular
weight x l0-3 |
Molecular
dimensions (nm) |
| Water | 90 - 92 | ||
| Proteins | |||
| Serum albumin | 3.3 - 4.0 | 69 | 15 x 4 |
| a1 globulins
(including lipoproteins) |
0.31 - 0.32 | 44 - 200 | |
| a2
globulins
(including glycoproteins) |
0.48 - 0.52 | 150 - 300 | |
| b globulins
(including lipoproteins) |
0.78 - 0.81 | 90 - 1300 | 20 - 50 |
| g globulins | 0.66 - 0.74 | 160 - 320 | 23 x 4 |
| Fibrinogen | 0.34 - 0.43 | 400 | 50 - 60 x 3 - 8 |
| Inorganic constituents | |||
| Cations | |||
| Sodium | 0.31 - 0.34 | ||
| Potassium | 0.016 - 0.021 | ||
| Calcium | 0.009 - 0.011 | ||
| Magnesium | 0.002 - 0.003 | ||
| Anions | |||
| Chloride | 0.36 - 0.39 | ||
| Bicarbonate | 0.20 - 0.24 | ||
| Phosphate | 0.003 - 0.004 | ||
It was noted in Chapter 1 that the physical features of liquids, gases, and solids are directly related to their molecular structure and that both liquids and gases are classed as fluids, because they flow when a shear stress is applied. The property which relates the rate of shearing to the shear stress is the viscosity (§4.3) and we must now consider the factors that determine the viscosity of a fluid.
It helps in understanding the physics of a liquid if at the same time we consider a gas. Gases are much less dense than liquids, and therefore the molecules of a gas are farther apart than those of a liquid. Thus they change location, by random motion, with greater ease because they collide less frequently. This is also associated with the fact that diffusion coefficients in gases are typically 10,000 times greater than in liquids.
Because of this large difference in the mobilities of the molecules in gases and liquids their viscosities arise in differing ways. For the case of a gas, imagine two parallel streams moving at different average speeds. Within each stream individual molecules are moving in random directions and with a wide spectrum of velocities. Some of the molecules will inevitably cross the plane separating the streams and be forced, by successive collisions with molecules in the stream they join, to speed up and hence adapt towards the average speed of the faster stream. At the same time'molecules moving in the opposite direction, across the plane of separation, will be slowed down. Thus the difference in relative velocity of the two streams is reduced. The manner in which its molecules migrate determines the viscosity of a gas; for example, when its temperature is raised, the thermal agitation of its molecules becomes more intense, and so its viscosity rises.
We may think of a liquid as possessing a molecular structure somewhere intermediate between the ordered form of a crystalline solid and the completely random form of a gas. As a solid melts to form a liquid its lattice structure breaks down, but small clusters of molecules with a coherent structure are still present. As the liquid temperature is raised the increased vibrational energy of molecules within a group causes it to be progressively broken down in size, till at the boiling point the liquid possesses virtually no such groups.
The viscosity of a liquid is very many times higher than that of a gas both because the molecules are packed more closely together and because the relatively large coherent groups provide an increased resistance to deformation. Unlike the situation in gases, the viscosity of liquids decreases with increasing temperature. This is thought to result from the progressive breakdown of the coherent groups despite the effect of increasing mobility of individual molecules within the liquid.
When a suspension of randomly distributed particles (be they rigid, deformable, or fluid) is flowing in an apparatus whose dimensions are large compared with those of the particles and the spaces between them, the mixture can be regarded as a homogeneous fluid, as discussed in Chapter 1. By studying the mechanical properties of such a suspension, we can begin to see what determines its viscosity and whether it behaves in a Newtonian fashion. Newtonian behaviour is denned in Chapter 4 (§4.3). We can begin to see, furthermore, what factors determine the viscous behaviour of blood.
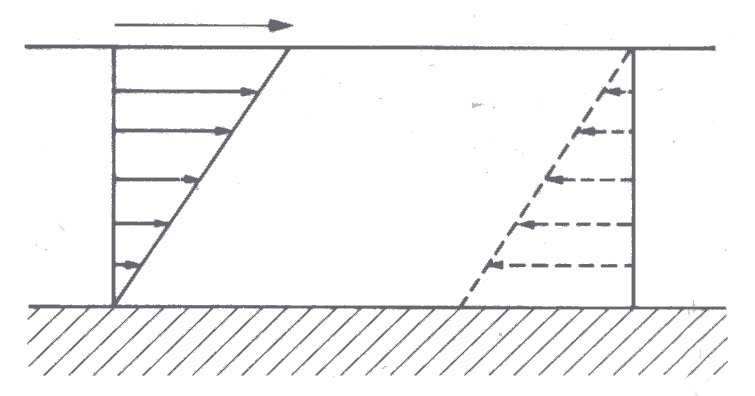
10.1.1 Spherical particles. If the suspended particles are spherical and non-settling, that is, have the same density as the suspending fluid, which is itself Newtonian, then in any motion the shear stress will be proportional to the strain rate (rate of shear) and the suspension will behave as a Newtonian fluid, unless the concentration of spheres is very high. This is borne out by experiments under steady-state conditions, with suspensions of rigid spheres, as described in §13.5.1. The effective viscosity ms of the suspension, which is its viscosity when measured in a particular viscometer under particular conditions (see also §10.6.3), is independent of the shear-rate for volume concentrations c of suspended spheres as high as 30 per cent. However, for concentrations greater than about 10 per cent the effective viscosity depends on the method of measurement, that is, on the flow pattern in the viscometer. Therefore, when it is said that a suspension of rigid spheres is Newtonian, what is usually meant is that its viscosity, as measured in a particular way, is independent of shear-rate. If the suspended particles are not spherical, or are deformable, or are attracted to one another and tend to aggregate, then the shear stress is not proportional to the shear-rate unless the concentration is much less than 30 per cent. A suspension of red cells in plasma, for example, shows a shear-dependence of viscosity at concentrations greater than about 12 per cent (Fig. 10.16). The effective viscosity of a suspension always exceeds that of the suspending fluid. To see that this must be so, consider a Newtonian fluid in which motion is caused by motion of its boundaries at a steady rate as in Fig. 10.1.

Fig. 10.1. Steady shearing of a Newtonian fluid between parallel plates. There is no slip of the fluid at either boundary (§4.4). The lower plate is stationary with respect to the observer and the length of the arrows indicates fluid velocity with respect to it. Clearly for an observer riding with the upper plate the fluid and lower plate would appear to be travelling in the opposite direction (dotted diagram). There is a linear change in velocity from one boundary to the other and as a result a constant or uniform velocity gradient (see Chapter 4).
The fluid will be sheared between the moving boundaries, and as a result of this shearing, energy will be dissipated at a rate proportional to the viscosity of the fluid.
Now suppose that rigid spherical particles are introduced (Fig. 10.2).
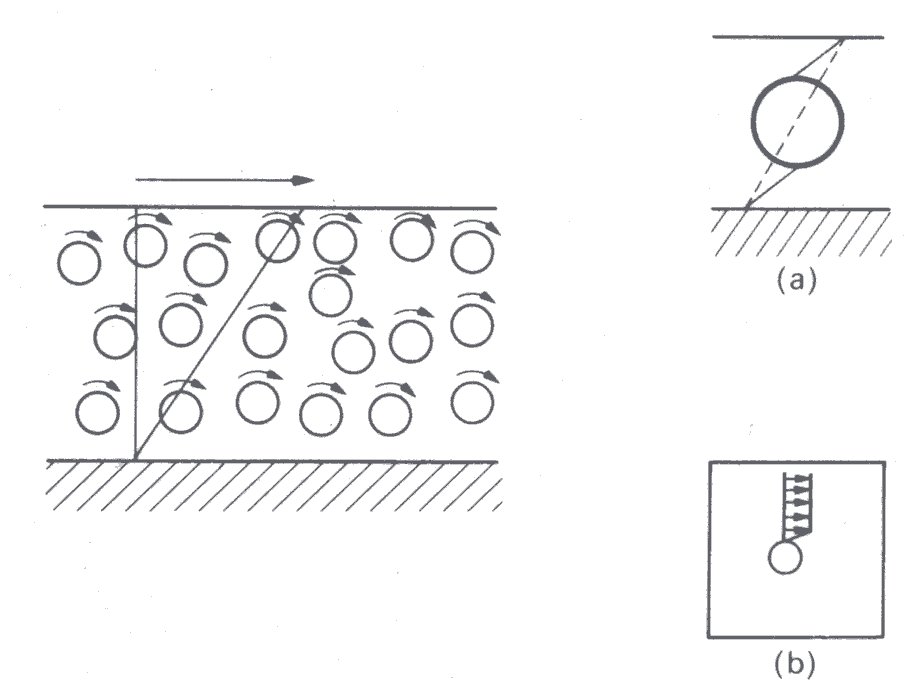
Fig. 10.2. Shearing of a suspension of rigid spherical particles. There is rotation of the particles, but as shown (insert (a)) for a given motion of the boundaries the presence of a rigid particle causes an increased rate of shear in the fluid. It is also seen (insert (b)) that there is a velocity gradient in the fluid adjacent to the particles, because fluid cannot slip at their surface.
These may rotate in the fluid, but they cannot deform in the same way as did the fluid whose volume they occupy. Therefore, deformations in the fluid must be greater for the same motion of the boundaries, and the average shear-rate in the fluid increases. Furthermore, since fluid on the surface of the particles cannot slip (Chapter 4, §4.3), there is additional shearing in the fluid close to the particles. Both these effects lead to an increased rate of energy dissipation within the fluid, so that its effective viscosity is increased. As the volume fraction c of suspended particles increases, one would expect the effective viscosity to increase still farther, and this is borne out by experiment. However, unless the concentration of particles is very high the relationship between shear-rate and shear stress at any given concentration is constant - i.e., the fluid is Newtonian.
A suspension of liquid drops or deformable particles also shows an increase in viscosity with increase in volume fraction, though it is smaller in amount for a given increase in concentration than in the case of rigid particles. This is because the drops can accommodate some of the deformation and the additional rate of strain imposed on the suspending fluid is therefore less. However, as the shear-rate increases in such a suspension the drops not only deform, but also progressively align with the flow (Fig. 10.3).
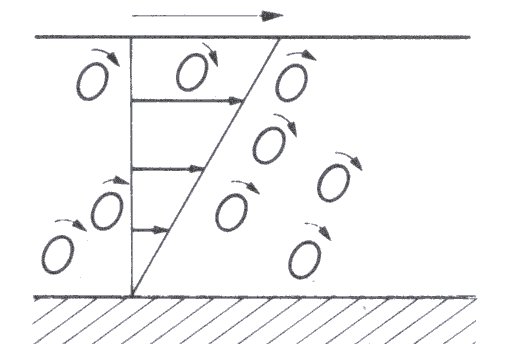
Fig. 10.3. Shearing of a suspension of liquid or deformable particles. The particles rotate as in Fig. 10.2 but also become deformed and orientated in the direction of motion.
This means that the shear stress does not increase linearly with shear-rate; thus the viscosity shows dependence on shear-rate and the suspension is therefore non-Newtonian. This topic is dealt with in more detail shortly when we consider the behaviour (also non-Newtonian) of rigid non-spherical particles in suspension.
The behaviour of suspensions of rigid or deformable particles may also be complicated and rendered non-Newtonian by interaction between the particles, due to fluid disturbed by one particle disturbing the motion of another, or to attractive or repulsive forces between the particles themselves. The only exact theory we have relates to dilute suspensions of non-interacting particles. The effective viscosity ms of a dilute suspension of equal sized, rigid, non-interacting, neutrally buoyant, spherical particles in a fluid of viscosity m0 was calculated first by Albert Einstein, in 1906. He predicted that, provided the volume concentration c of particles is small compared with 1, the relative viscosity of the suspension mr, which is the ratio of its effective viscosity to that of the suspending fluid, is given by
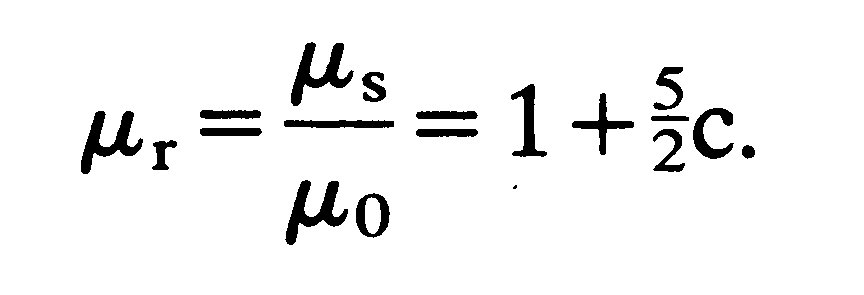 (10.1)
(10.1)
This result has been verified by experiment for values of c less than about 0.1. For greater values the complicated mutual interaction of particles has to be taken into account and this involves terms proportional to c2. In 1932 Einstein's result was extended by G. I. Taylor to suspensions of liquid drops, which are forced to remain spherical, for example by surface tension. The result corresponding to Equation (10.1) is
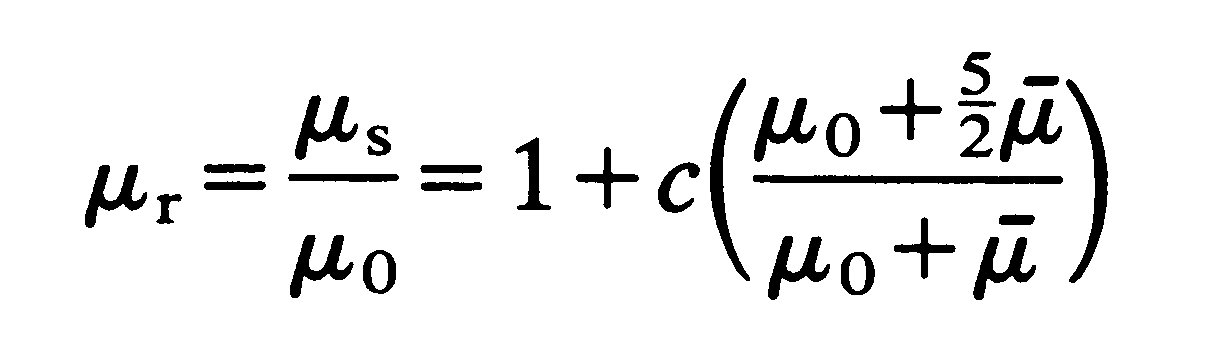 (10.2)
(10.2)
where m is the viscosity of the liquid in the drop. This reduces to Equation (10.1) as m becomes infinite, i.e., as the drop becomes effectively rigid.
10.1.2 Asymmetric particles. The shearing of a suspension of rigid spherical particles causes the particles to rotate with constant angular velocity. If however the suspension consists of asymmetric particles, then, though they rotate when the suspension is sheared, they are found to do so with a time-varying angular velocity. The angular velocity of an asymmetric particle is highest when its long axis is at right angles to the direction of the flow and lowest when it is parallel with the flow. It can be seen therefore that the particle spends most of its time with its long axis roughly parallel to the plane of shear. The effect of this 'lining-up' of the particles by the shear force is to decrease the viscosity of the suspension, making its behaviour non-Newtonian.
The relative viscosity of a suspension of randomly orientated rigid asymmetric particles exceeds that of a suspension of rigid spherical particles at the same volume concentration c. This is because, during the tumbling motion induced by the shear force, each particle sweeps out a volume of fluid greater than its own volume, but which is intermediate between those predicted from its longest and shortest dimensions (Fig. 10.4).
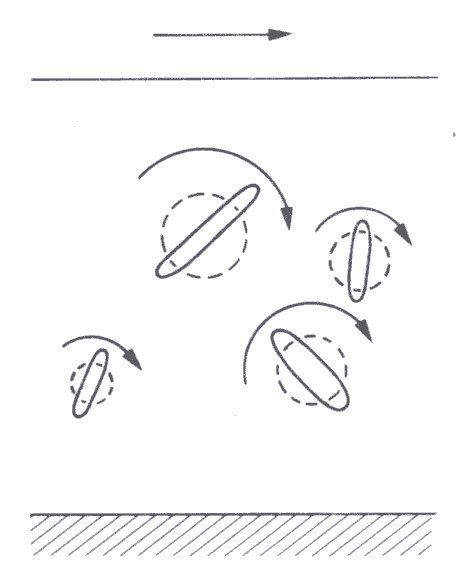
Fig. 10.4. Tumbling motion of asymmetric particles in a sheared suspension with schematic representation of the swept volume for each particle.
The relative viscosity of a suspension of rigid asymmetric particles increases both with increasing concentration and increasing asymmetry of the particles. The relationship is given by
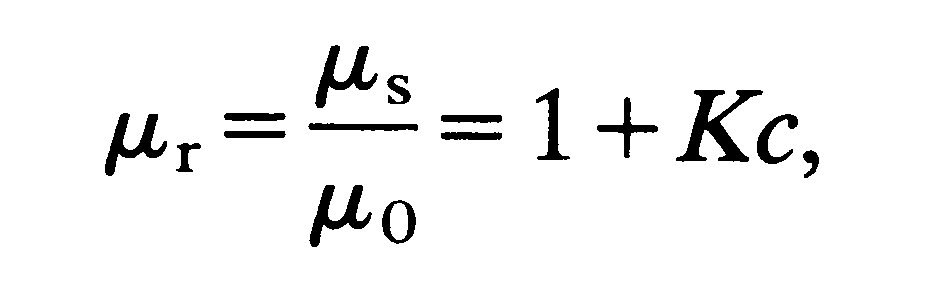 (10.3)
(10.3)
where K (a geometric factor) is greater than 5/2 (see Equation (10.1)) and increases as the asymmetry of the particles increases.
A further complication occurs if the asymmetric particles are flexible. For reasons which we need not explore here they will tend to bend during part of their cycle of rotation in a sheared flow (Fig. 13.24). As a result the volume of fluid they sweep out is decreased as the shear-rate goes up, and hence so is the effective viscosity of the suspension.
Under suitable conditions of particle size, temperature, and viscosity of the suspending fluid, Brownian motion (§9.1) will ensure that asymmetric particles in suspension are randomly orientated. As we have seen, the shearing of such a suspension will reduce its effective viscosity, if the rate of shear is sufficiently high to overcome this effect of Brownian motion. This behaviour is of interest because blood plasma contains an appreciable amount of such proteins as fibrinogen and the globulins, which have markedly asymmetric molecules. These molecules are so large compared with those of water that they may reasonably be regarded as being in suspension, and might therefore impart non-Newtonian properties to the plasma. In practice, as we shall now see, this does not happen.
10.1.3 Viscosity of plasma. Plasma is a pale yellow transparent fluid, which is obtained by removing the cells from blood that has been prevented from coagulating. Typical values for the concentrations and dimensions of some constituents of normal human plasma are given in Table 10.1; the materials selected are those particularly likely to influence the mechanics of plasma, or whole blood. Serum has the same appearance as plasma, but is obtained by allowing blood to coagulate and removing the clot. Thus it lacks the plasma constituents involved in clotting, in particular fibrinogen.
Normal plasma behaves like a Newtonian fluid at rates of shear comparable with those in vivo (§12.9.2), provided that precautions are taken during viscometry to eliminate an air-plasma interface, and thus prevent denaturation of the proteins and mechanical effects due to the interface. This confirms theoretical predictions that there should be an immeasurably small influence of shear-rate on plasma viscosity, in the normal range; it seems therefore that Brownian motion maintains a random orientation of the asymmetric molecules at these rates of shear. Typical values for the viscosities of normal human plasma and serum, at 37 °C, are 1.2 and 1.1 mN s m-2. The viscosity of plasma is increased in certain diseases, for example in multiple myeloma, a malignant disease of the globulin forming cells in the bone marrow, when the plasma concentration of globulins may be raised several fold. It is not at present certain whether this abnormal plasma behaves as a Newtonian fluid.
The viscosity of normal plasma varies with temperature in just the same way as does that of its solvent, water; a 5 °C increase of temperature, in the physiological range, reduces plasma viscosity by about 10 per cent (Fig. 10.5).
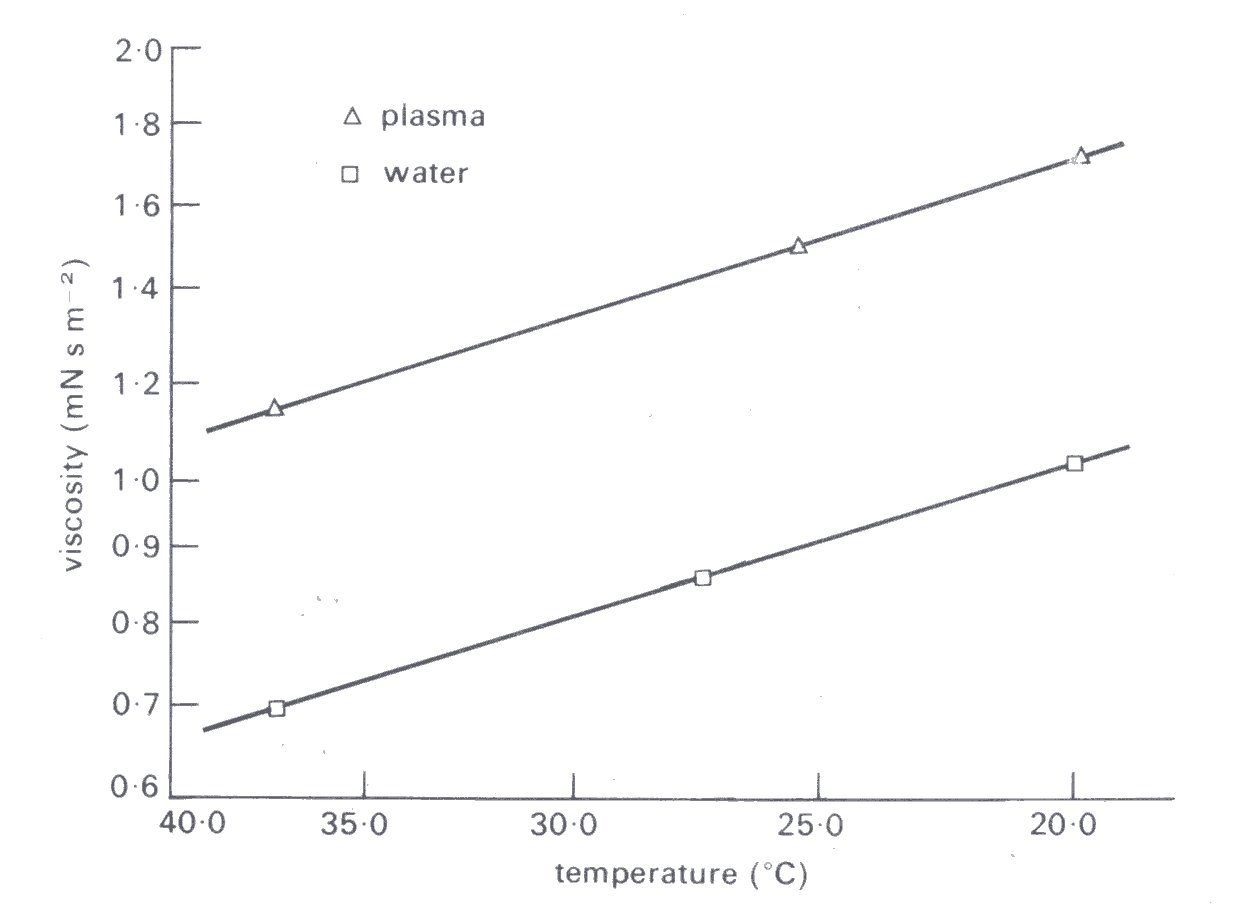
Fig. 10.5. Temperature dependence of plasma viscosity compared with that of water. (After Cokelet (1972). "The rheology of human blood'. In Biomechanics, its foundations and objectives (ed. Fung, Perrone, and Aniiker), Chapter 4. Prentice-Hall, New Jersey.)
We set out in Chapter 9 the physical basis of osmotic pressure and now provide some quantitative information on the osmotic properties of plasma. We also begin to examine the influence of plasma osmotic pressure on the mechanics of the circulation.
The osmotic pressure of a solution is determined by the number of particles present and by the temperature. As an example, a one molar solution of a substance (1 mol dissolved in 1000 g of water) contains 6.02 x 1023 molecules and has, at 0 °C, an osmotic pressure of 2.27 MN m-2 (22.4 atm). Body fluids, however, contain both electrolytes and non-electrolytes and the former dissociate into ions in water. Thus with complete dissociation, a one molar solution of sodium chloride in water yields 12.04 x 1023 ions and has, at 0 °C, an osmotic pressure of 4.54 MN m-2 (44.8 atm). A litre of a one molar solution of a non-electrolyte contains one osmole and that of a similar solution of an electrolyte, such as sodium chloride, two osmoles, if dissociation is complete.
The osmotic pressure of the plasma affects the mechanics of the circulation in several ways. An alteration of the osmotic pressure difference across the membrane of a blood cell will cause a shift of water and a change of the cell volume. For example, a reduction of the concentration of sodium chloride external to red cells will cause them to swell. An extreme case is the sphered red cell, which is much stiffer than the normal disc-shaped cell, because of its inability to deform without stretching its membrane (§10.3.2). The change both in shape and flexibility will affect the mechanical properties of whole blood, as we shall see later in this chapter (§10.6.3). Furthermore, a change in plasma osmotic pressure will alter the haematocrit, the volume concentration of red cells in whole blood (§10.3.1) by redistributing water between the intravascular and extravascular spaces. This in turn will alter the mechanics of whole blood.
It is customary to describe a solution which has the same osmotic pressure as normal plasma (approximately 0.7 MN m-2 at 0°C) as being isotonic, and solutions with higher or lower osmotic pressures as being respectively hyper- or hypotonic. The colloid osmotic pressure is another commonly used term, applied to the osmotic pressure due to the presence of macromolecules, as opposed to small molecules or ions. There is a small colloid osmotic pressure difference between intravascular and interstitial fluid, i.e. across the walls of the capillaries, because there is less protein in the latter. It is this pressure difference, together with the transcapillary hydrostatic pressure difference, which largely determines the equilibrium distribution of fluid between the intravascular and interstitial compartments (§13.7.1). It is albumin which mainly determines the colloid osmotic pressure of plasma. The contribution of fibrinogen to the osmotic pressure is very slight because its molar concentration and hence its osmotic pressure are only about one fiftieth those of albumin.
The elements suspended in plasma are the blood cells, and the liquid droplets called chylomicrons. These droplets, which have diameters in the region of 0.2 - 0.5 mm, are part of the fat transport mechanism of the circulation. They are present, however, in such low concentration as to have no significant effect on the viscosity or osmotic pressure of the plasma. We discuss them, therefore, no further than to mention that they are principally present after fatty meals, enter the circulation from the lymphatics of the intestines, and are removed by mechanisms which include transfer of the fat to water soluble carrier molecules, the lipoproteins (Table 10.1).
10.3.1 The blood cells. Several types of cell are present in the circulating blood, but we focus attention particularly on the erythrocytes, or red cells, because they are the only cells which significantly influence the mechanical properties of blood. They do this because they are present in such high concentration (approximately 5 million mm-3) comprising about 45 per cent of its volume (Table 10.2).
Table 10.2 Cells in blood |
|||
| Cell | Number per mm3 | Unstressed shape and dimensions (mm) |
Volume concentration (%) in blood |
| Erythrocyte | 4 - 6 x 106 | Biconcave disc 8x1-3 | 45 |
| Leucocytes | Roughly spherical 7-22 | 1 | |
| Total | 4 - 11 x 103 | ||
| Granulocytes | |||
| Neutrophils | 1.5 - 7.5 x 103 | ||
| Eosinophil | 0 - 4 x 102 | ||
| Basophil | 0 - 2 x 102 | ||
| Lymphocytes | 1 - 4.5 x 103 | ||
| Monocytes | 0 - 8 x 102 | ||
| Platelets | 250 - 500 x 103 | Rounded or oval 2-4 | |
For comparison there are normally only 1-2 white blood cells, or leucocytes, per thousand red cells. The platelets are more numerous than the leucocytes (50-100 per 1000 red cells); but they have a negligible effect on the mechanics of normal blood, compared with the red cells, because they are so small; the volume of a platelet is only about one tenth that of a red cell, as may be seen from Table 10.2.
10.3.2 Red cells. We must briefly consider some aspects of the physiology of the red cells, before examining their mechanical properties. Virtually all of the haemoglobin in blood (about 15 g per 100 ml) is within the red cells. It is the haemoglobin (m.w. 67,000), consisting of the protein globin united to the iron containing organic molecule haem, which gives the cells their red colour, and because of its ability to combine reversibly with oxygen, endows blood with its large capacity for carrying oxygen. The O2 capacity of whole blood at sea level is about 20 ml per 100 ml, whereas that of plasma is only about 0.3 ml per 100ml.
The red cells are formed in the bone marrow and when immature they possess nuclei. The nucleus is, however, shed in most mammals as the cell matures, and nucleated red cells are normally absent from the circulating blood. Despite the lack of a nucleus, and of mitochondria,* red cells are metabolically active. Studies with isotopically labelled red cells show that their average life span is about 120 days. The maintenance of a steady concentration of the red cells in blood requires therefore that about 0.8 per cent of the total population is destroyed and formed daily. Apparently red cells become more fragile as they age, and it seems that they are destroyed, in vivo, partly by mechanical fragmentation and partly by engulfment by white blood cells and other 'scavenger' cells, a process called phagocytosis (§10.3.4). The mechanical fragmentation of the cells is believed to occur mainly in the microcirculation; it is there that the blood is subjected to the highest levels of shear stress (§12.9.2). We shall be devoting a lot of attention to the mechanics of the red cell, because of its important contribution to the mechanics of whole blood. However, the study of red cell mechanics has proved a difficult field and there is still lack of agreement on several subjects. [*These bodies are major intracellular sites of metabolic activity particularly involving oxidative energy release.]
When suspended unstressed in plasma, or other isotonic fluid, the red cell is a highly flexible bi-concave disc with the shape and dimensions shown in Fig. 10.6.
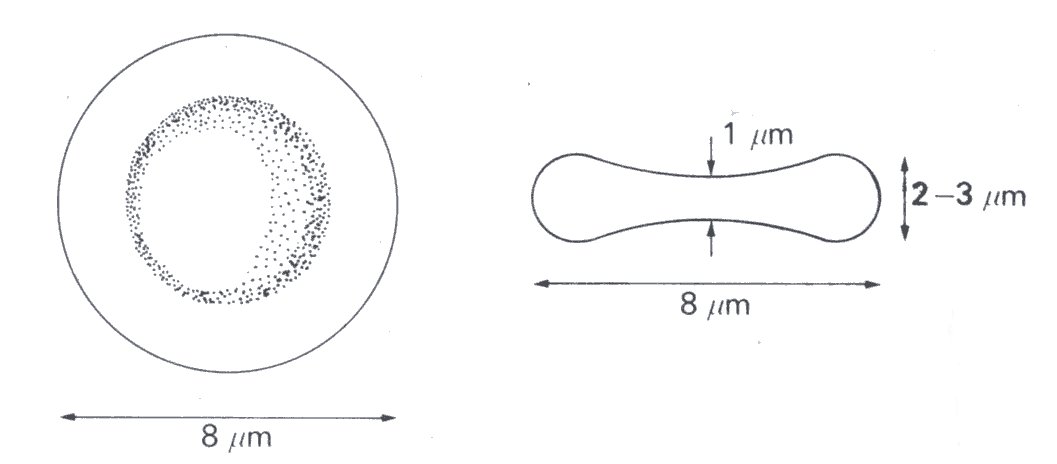
Fig. 10.6. Diagram of an unstressed erythrocyte.
Its density is approximately 1.08 x 103 kg m-3 and it is believed to consist of a very thin membrane and a liquid interior, which is apparently an almost saturated solution (approximately 32 per cent by weight) of haemoglobin; we shall review the evidence for these properties later. Some of the components of the red cells are listed in Table 10.3. The viscosity of the fluid interior is thought to be about 6 mN s m-2, which is about five times greater than that of blood plasma. It is suggested that this may alter in some diseases, such as sickle cell anaemia (§10.6.3), when the haemoglobin may become crystalline.
Table 10.3 Composition of the red cell |
|
| percentage of mass | |
| Water | 65 |
| Membrane components (protein, phospholipid, cholesterol) | 3 |
| Haemoglobin | 32 |
| Inorganic: | |
| Potassium | 0.420 g per 100 ml |
| Sodium | 0.025 g per 100 ml |
| Magnesium | 0.006 g per 100 ml |
| Calcium | small amount |
Studies of the red cell membrane suggest that it contains a phospholipid bi-layer, about 7.5 nm in thickness. The membrane accounts for no more than 3 per cent of the mass of the cell, is highly permeable to the anions chloride and bicarbonate, and to water, but has a very low permeability to the cations potassium and sodium, and to macromolecules, including the plasma proteins. The cell possesses a Na+- K+ exchange pump, that pumps Na+ out and K+ in, against electro-chemical gradients (compare Tables 10.1 and 10.3). It metabolizes glucose to produce energy for this pump and, because it lacks mitochondria, this metabolism is primarily anaerobic.
Several observations support the notion that the interior of the red cell is liquid. For example, the cell is capable of extreme distortion, as when it travels along a capillary with a diameter smaller than its own. The form that it then adopts, blunt in front and sharpened at the rear (Fig. 13.33 (a)), suggests that there has been a flow of its contents into the blunt forward part. A similar conclusion is reached after a study of the behaviour of a red cell that has been made to adhere to a glass microscope slide by coating the slide with serum albumin. If the adherent cell is exposed to a shear stress it deforms (Fig. 10.7),
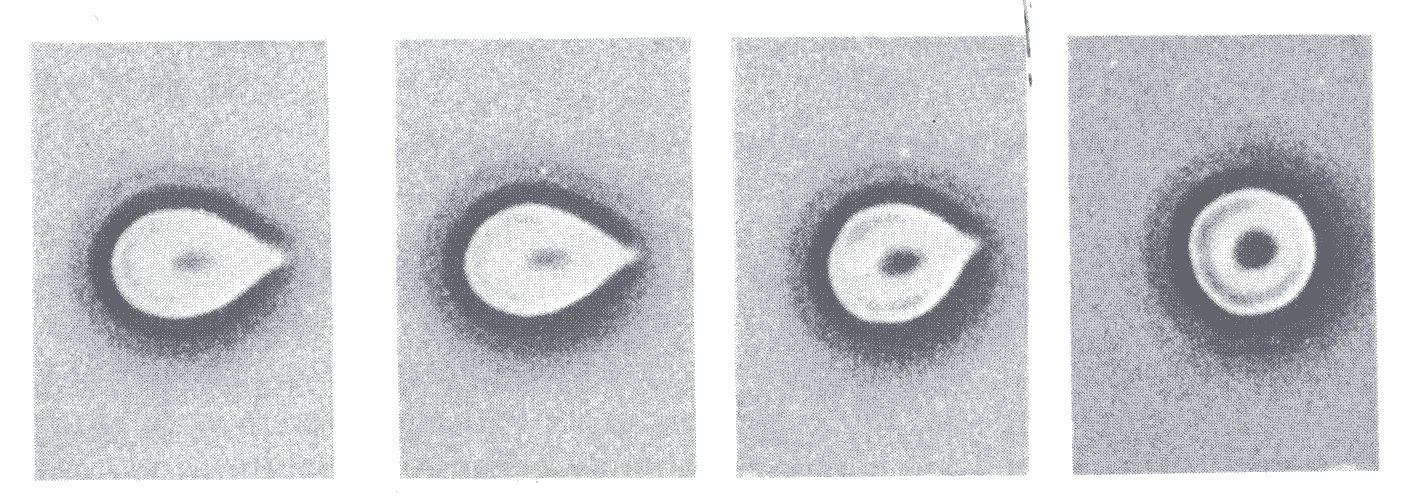
Fig. 10.7. Red cell made to adhere to a glass slide and then subjected to a shearing stress. The direction of the flow is from right to left and the level of the shear stress is greatest in the left-hand. (From Hochmuth, Mohandas, and Blackshear (1973). Biophys. J. 13, 754.)
and with increase of the shear stress it elongates and the cell contents appear to be squeezed out of the stretched tail into the cell body.
These and other observations (including electron microscopy) indicate that intact cells have no internal structure, that is, that the contents of the red cell are liquid. They suggest furthermore that the shape of the red cell is determined by the properties of its membrane. Support for that view comes from observations with red cell ghosts. If the osmotic pressure of the fluid in which red cells are suspended is gradually lowered, they not only become spherical, but lose their contents, first the low molecular weight materials and then, through rupturing of the membrane, the haemoglobin, a process known as haemolysis. If cells ruptured in this way are placed in a suitable isotonic solution the membrane seals, they absorb the solution and return closely to resemble normal red cells in shape and size. The name ghost arises because of the lack of haemoglobin.
There is, however, one piece of experimental evidence which has been used to suggest that the red cell has an internal structure; it can be cut into fine pieces, without losing its contents. To account for this observation it has been suggested that the cell interior contains a network of flexible material. However, neither electron microscopy nor ghost studies provide any support for this; possibly the cell membrane seals about the fragments as they are formed.
Since the thickness of the cell membrane is only some 7.5nm, and the smallest radius of curvature of the red cell is about 1 mm (Fig. 10.6), thin shell theory can be applied to examine its behaviour. This predicts that the membrane has negligible stiffness to bending, compared to its stiffness on stretching (see also §13.6). As a result, if the interior of the cell is liquid and hence able to offer viscous, but not elastic, resistance to deformation, the cell is expected to be very flexible.
The great ability of the red cell to deform (it can, for example, traverse a tube 3 mm in diameter and 12 mm in length without rupturing) is due, however, as much to its shape as to the properties of the membrane and to the liquid interior. Like other non-spherical bodies, the bi-concave red cell can deform into an infinite variety of shapes without changing its volume or surface area, that is, without stretching its membrane. The significance of this is most readily appreciated if one compares the mechanics of a normal and a sphered red cell. It can be shown that a sphere contains the maximum volume for a given surface area. Thus the area of a sphered cell's membrane must increase if the cell is deformed, so that the tangential stiffness of the membrane determines the cell's flexibility. It is indeed found experimentally that sphered red cells cannot deform to the same extent as normal ones, and cannot, for example, traverse the same narrow channels without rupturing. However, with very severe deformation as in a highly sheared flow, the membrane will become tense, tending to limit deformation of the cell, and may rupture as described below.
The Young's modulus of the red cell membrane has been determined and is in the region of 106 N m-2. These measurements were made with the membrane stretched nearly to breaking point, and most biological tissues exhibit an increasing Young's modulus with increasing strain (see Chapter 7). Studies in which the motion of a red cell, as it returns to its unstressed shape after deformation, is compared with that of a scaled model cell whose properties are known, yield a value for the Young's modulus of the membrane of about 105 N m-2, that is, less by a factor of ten.
The red cell membrane has the property that however it is deformed it appears to maintain a constant surface area and thickness. For example, there is no observable change in surface area when a red cell is sphered osmotically. On the other hand red cells elongate markedly when they are exposed to a high shear stress, as during tethering experiments (Fig. 10.7), or in a viscometer (Fig. 10.9).
We have not so far attempted to explain why a red cell which has a liquid interior and possesses a disc shape when suspended unstressed in an isotonic solution is capable of swelling and sphering. Theoretically a cell whose membrane is uniformly extensible cannot behave in this way. As illustrated in Fig. 10.8,
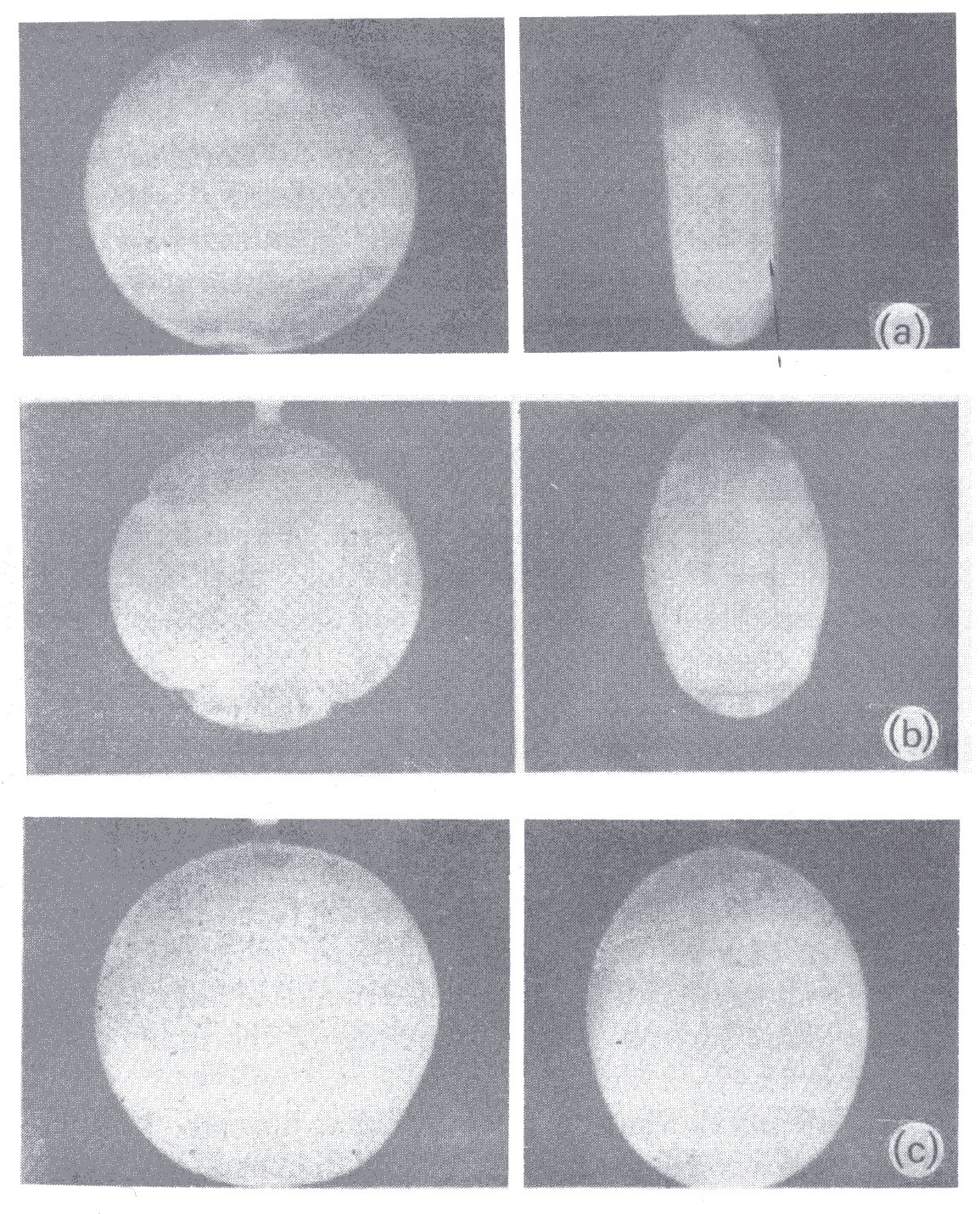
Fig. 10.8. (a) Thin-walled rubber model of red blood cell filled with water and immersed in water. With increase of transmural pressure (b) the poles bulge out and there is buckling at the equator. At large internal pressure (c) the enlarged cell is smooth again and almost spherical. (From Fung (1966). 'Theoretical considerations of the elasticity of red cells and small blood vessels'. Fedn. Proc. Fedn. Am. Socs. exp. Biol. 25, 1761-72.)
the change from a disc to a sphere requires a reduction of the circumference of the cell at its equator and hence wrinkling there, as the poles pop out. This is actually seen with a model red cell which has uniform membrane properties, but not with real red cells. The observed behaviour of the red cell on sphering can be explained if the Young's modulus of the membrane and/or its thickness is greater at the equator than at the poles, but there is as yet no direct evidence on this point.
We now turn to the deformation of red cells which is induced by shear stress and consider observations that have been made when a sheared flow is set up in a dilute suspension of red cells. It is obvious that a cell must deform if it is to enter a very narrow tube and flow along it, and it will be apparent from the discussion of non-rigid suspended particles earlier in the chapter that a blood cell must deform in a sheared flow. Direct observations with a travelling microscope confirm this (Chapter 13). When a suspension is sheared the red cells are seen to deform and spin, because of the velocity gradient (shear-rate), but the rate of deformation and spin depends on the shear-rate and the concentration. At a shear-rate of about 1 s-1 the cells bend as they spin, but with increase of the shear-rate they cease to spin as a whole and instead travel down the tube with their major axis at an angle to the flow. Close examination suggests that they then have constantly changing contours, consistent with rotation of the cell membrane about the interior, rather like the moving tread of a tank. In that case the cell would be behaving to some extent like a liquid droplet (§10.1.1).
Experiments with laminar flow have suggested that a shear stress of about 200 N m-2 is required to haemolyse red cells, but this level is uncertain and some workers claim that it is contact with foreign surfaces, rather than the level of the shear stress, which primarily causes haemolysis. Fig. 10.9 (a) and (b) are electron micrographs of very dilute (0.2 per cent) suspensions of human red cells, fixed by glutaraldehyde while being subjected to different levels of shear stress in a concentric cylinder viscometer.

Fig. 10.9. Red cells fixed with glutaraldehyde while being subjected to a shearing stress in a viscometer. The stress is 10 N m-2 in (a) and 300 N m-2 in (b). (From Sutera, Mehrjardi, and Mohandas (1974), personal communication.)
There is mild deformation of the cells at 10 N m-2, but marked deformation at 300 N m-2, when the cells are greatly elongated (up to 20-30 mm). When the cells were fixed after the shear stress had been returned to zero, most had a normal appearance, implying that they had suffered no permanent change. 200 N m-2 is, however, probably a very high shear stress for the circulation; a shear stress of 40 N m-2 will rupture or tear away the endothelial cells which line the aorta. In intensely turbulent flow, such as may occur downstream of a stenosed aortic valve, haemolysis is also thought to take place, accounting for the anaemia sometimes seen in this condition. However, the magnitude and duration of the shear stresses in this situation remain unknown.
A further property of red cells is their tendency to aggregate. If blood is smeared on to a microscope slide the red cells can be seen to attach themselves side-by-side to form what are described as rouleaux (Fig. 10.10).
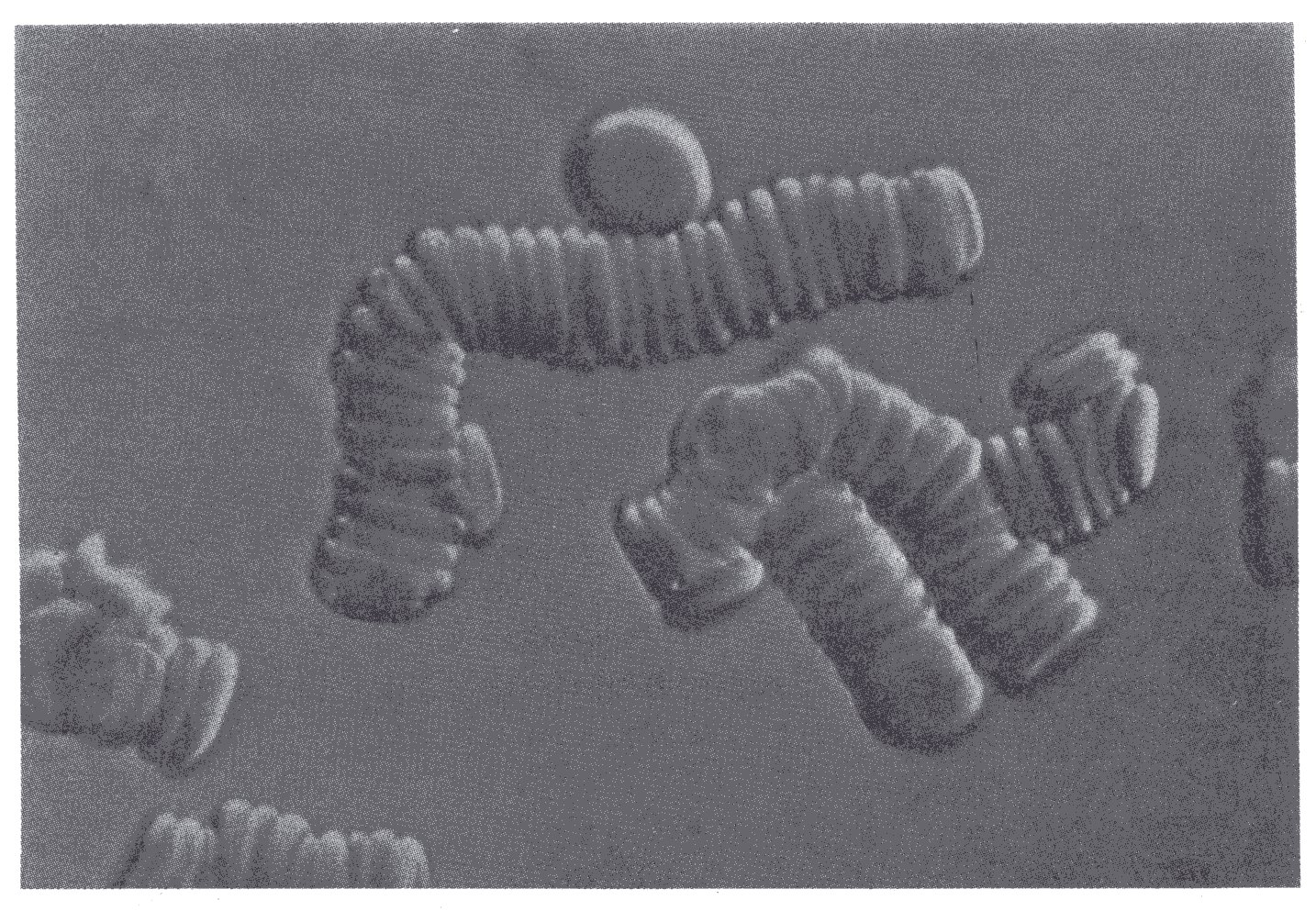
Fig. 10.10. Profile view of erythrocytes forming rouleaux. (From Bessis (1973). Living blood cells and their ultrastructure (tismsl.'Weed), p. 141. Springer Verlag, Heidelberg.)
This process begins after 10-20 s, and the rouleaux continue to increase in length for 1-2 min. The mechanism of rouleaux formation is still incompletely understood. It appears that the red cells attract one another and that the attraction is determined by charged groups on the surface of the cells. The process also depends on the presence of certain large asymmetric macromolecules in the external environment, particularly fibrinogen and globulins. The process will not occur in their absence, for example with red cells suspended in saline or serum albumin at normal concentration. Furthermore, it occurs progressively faster with increasing concentrations of fibrinogen and globulins. Thus in a steady sheared flow the proportion of the cells aggregated into rouleaux at any instant depends on the concentration of these materials.
The greatest diameter of red cells when studied in rouleaux exceeds the unstressed value and cell thickness is reduced correspondingly; this is consistent with the presence of attracting forces between the cells. Red cells which have been sphered or hardened, for example by glutaraldehyde, will not form rouleaux, possibly because of their inability to undergo the necessary deformation.
Rouleaux can develop in vivo, as well as in vitro, at low rates of shear and their formation shows the same dependence on the concentration of fibrinogen and globulins. They are important because of their influence on the viscosity of blood at low rates of shear (§10.6.3) and on its sedimentation velocity (§10.6.2).
10.3.3 White cells. We discuss the white cells, or leucocytes, only briefly, because of their very small effect on the mechanical properties of blood; they are present in blood in very low concentration, constituting about 1 per cent of its volume. They play a crucial role in defence against infection, both by acting as scavengers of micro-organisms and by forming antibodies. Details of these cells can be found in text books of physiology and haematology.
There are three varieties of white cell present in the circulating blood, the granulocytes, lymphocytes, and monocytes, though these varieties are subdivided (Table 10.2). The different cells can be distinguished by their microscopic appearance and their affinity for various organic dyes.
White cells are normally roughly spherical in shape, with the diameters of the different varieties of cell ranging from about 7 to 22 mm (Table 10.2). Electron microscopy shows extensive internal structure, including the presence of mitochondria; and judged on the basis of volume, white cells are considerably more active biochemically than are red cells, exhibiting both aerobic and anaerobic metabolism. They are capable of active amoeboid movement, in which they project pseudopodia. They are also capable of phagocytosis, the engulfment of foreign material, including bacteria and ageing or fragmented cells. Smaller particles from macromolecules downwards can also be taken up and extruded, but this occurs by a different mechanism, known as pinocytosis (§13.7.9).
Rather little is known of the mechanical properties of the white cells. It has been argued that they are stiffer than red cells, because in a collision between a red and white cell in flowing blood, it is the former which mainly deforms. There is a need, however, to take into account the visco-elastic properties of the cells. Thus it has been observed that where a white cell is caused to flow from a wide tube into a capillary, which is smaller than its unstressed diameter, 10-20 s are required before the cell has deformed sufficiently to flow along the capillary. White cells can be made to swell and rupture if they are placed in a suitable hypotonic solution.
10.3.4 Platelets. The platelets are formed in the bone marrow, from very large cells called megakaryocytes. When viewed in vivo, for example in a capillary, they are small round or oval bodies, 2-4 mm in diameter and with a volume of 5-10 mm3. They lack nuclei, but electron microscopy reveals a membrane about 8 x 10-3 mm thick, and inclusions similar to those found in other cells, including mitochondria, microfibrils, and microtubules.
If platelets come into contact with ADP (adenosine diphosphate, an organic molecule important in many energy releasing pathways in the body), they aggregate; ADP is regarded currently as the agent which normally promotes platelet aggregation in vivo. It is released from damaged red cells and connective tissue (collagen) at sites of injury, but its chief source for platelet aggregation is probably the platelets themselves, so that platelets adhering to damaged tissue may well release ADP for further platelet aggregation.
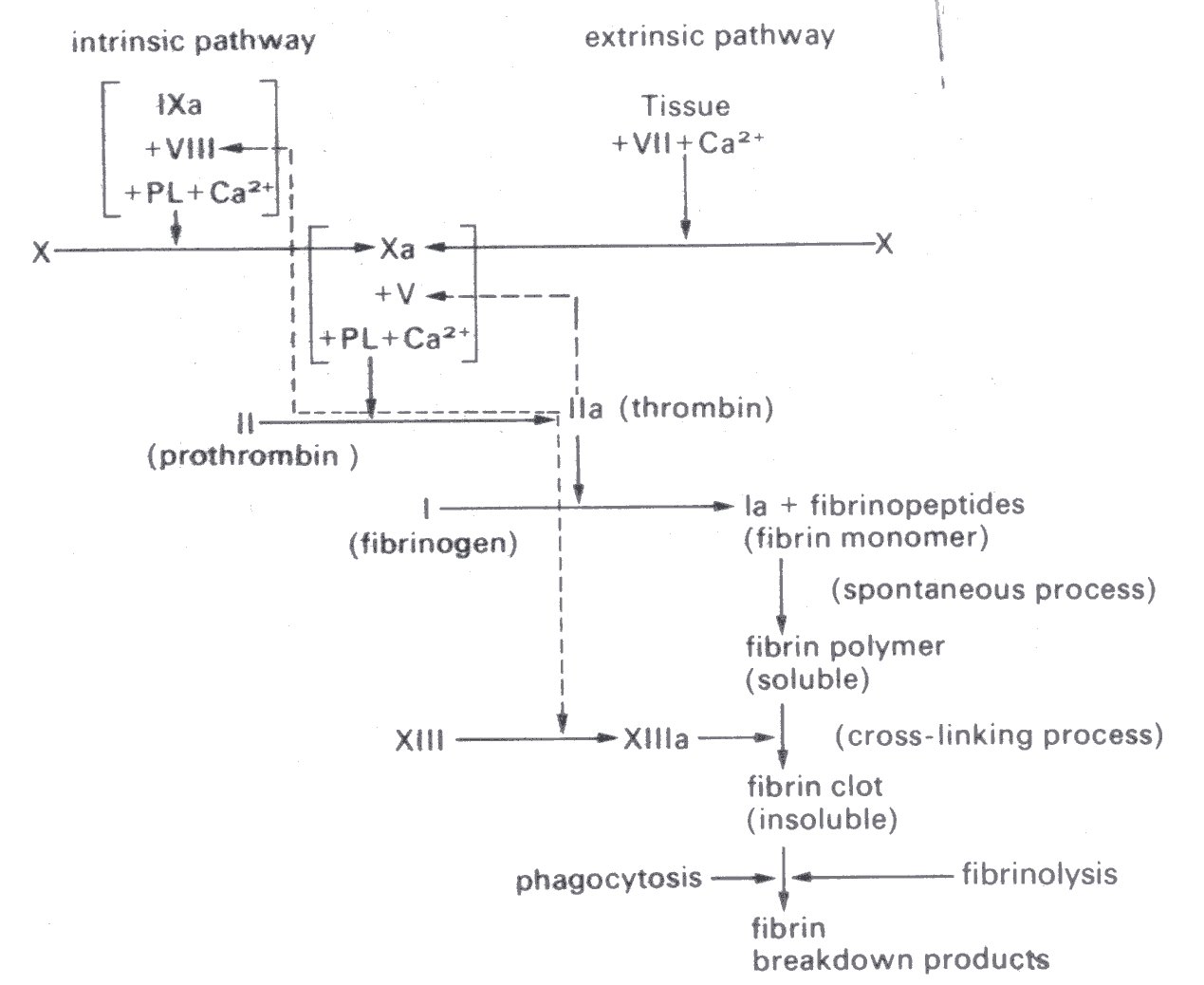
Fig. 10.11. Later stages of clotting process (see text). The factors are numbered according to the International nomenclature of clotting factors. Synonyms for those not identified on the figure are: V - proaccelerin; VII - proconvertin, or serum prothrombin conversion accelerator; VIII - antihaemophilic factor; IX - Christmas factor; X - Stuart-Prower factor; XIII - fibrin stabilizing factor. Activated derivatives are denoted by the suffix a. PL - plasma; Ca2+ - calcium ions. (After Hardisty and Weatherall (1974). "The haemostatic mechanism'. In Blood and its disorders. Blackwell Scientific Publications, Oxford.)
In the presence of thrombin (see next section, Blood coagulation, and Fig. 10.11), collagen, ADP, or adrenaline, platelets rapidly lose their rounded shape, putting out many small protuberances (pseudopodia). This shape change, which is reversible, precedes aggregation. When aggregation occurs the cells come into close contact, they extrude much larger pseudopodia (Fig. 10.12) and these changes are irreversible.
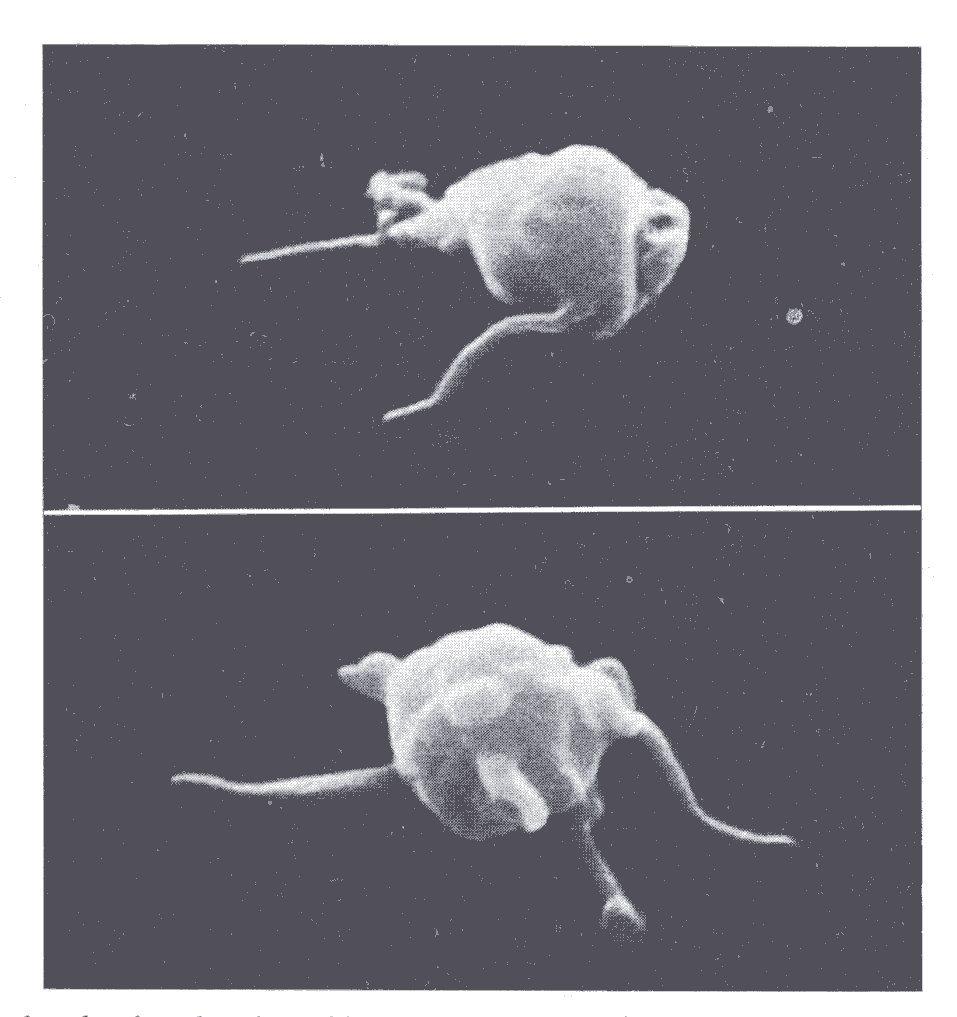
Fig. 10.12. Platelets having developed large pseudopodia (scanning electron micrographs). (From Bessis (1973). Living blood cells and their ultrastructure (transl. Weed), p. 381. Springer Verlag, Heidelberg.)
Platelet aggregation is one of a number of processes, including clotting and vascular constriction, which operate to stop bleeding from damaged or cut vessels; such processes form important body defences against injury. There is evidence to suggest that platelet aggregation is active also in plugging spontaneously occurring small leaks in the normal circulation.
Blood coagulates when it is in an abnormal environment, for example a glass test tube, a damaged blood vessel, or a wound. The process of blood coagulation is exceedingly complicated and still incompletely understood. We shall therefore set out only the essential stages.
A blood clot consists of a mesh of fibrils, which are composed of the protein fibrin, and red and white cells and platelets (in the same relative concentrations as in whole blood) entangled in the mesh. There is very little fibrin present in normal blood; it is produced during coagulation, as shown in Fig. 10.11. This figure merely illustrates the important stages as they are at present understood; it is based upon a recent review to which the reader is referred. Note that the penultimate major step (conversion of prothrombin to thrombin) can be activated by two pathways, one (extrinsic) depending on the release of clotting factors by tissue damage, and the other (intrinsic) dependent on the contact of blood with foreign surfaces. The anticoagulant substance heparin interferes with these pathways and also inhibits the reaction between thrombin and fibrinogen.
If fibrin is formed in blood vessels, in vivo, it may be removed either by phagocytosis or by being broken down, a process called fibrinolysis. Fibrinolysis, like fibrin formation, involves a complicated series of enzymic reactions.
After the formation of a clot it retracts, that is, the fibrin strands shorten, the clot becomes firmer, and serum is squeezed out. It seems that the platelets adhering to the fibrin strands are involved in this process. They have been shown to contain a contractile actomyosin-like protein, which is similar to that in muscle.
When blood coagulates in a blood vessel during life the process is called thrombosis. The process differs at different sites in the circulation, probably being strongly influenced by the local fluid mechanics. Thrombi, like clots, consist of the various elements of the blood trapped in a fibrin meshwork and the mechanism of production of the fibrin is probably similar to that in clotting, involving the chain of processes shown in Fig. 10.11. However, the initiating mechanism of thrombosis is usually somewhat different. Because of this and because of the fluid mechanical influence the structure of thrombi not only differs from that of clots but may also be different in different parts of the circulation. The closest resemblance to clotting occurs in venous thrombosis, especially if the blood flow is very sluggish; this type of thrombosis is particularly likely to occur in older patients who are undergoing surgery or are immobile in bed for long periods. In arteries on the other hand the structure of thrombi is different; the first portion of the thrombus to be formed, the 'head', is made up largely of aggregated platelets on which layers of fibrin and blood cells are subsequently deposited.
There are multiple causes of thrombosis and the process can occur anywhere in the circulation, but in arteries at least the crucial initial event is the formation of an aggregate of platelets. Blood platelets do not normally adhere to one another or to vessel walls, and as described earlier it appears to be the presence of ADP which initiates this. There are also grounds for suggesting that platelet aggregates and damaged tissue may produce material which can initiate blood clotting; these act via the 'extrinsic' pathway (Fig. 10.11). The local mechanics of flow may influence the process by affecting both the diffusion of the materials in the blood which are responsible for the platelet aggregation and clotting, and the supply of platelets and other cells to a site of thrombosis. Coagulation of blood within the circulation may be brought about experimentally by the injection of tissue extract or thrombin; thus it is possible that the levels of substances like ADP may, by causing platelet aggregation, influence the likelihood of thrombosis in vivo.
In arteries the commonest predisposing cause is atheroma (Chapter 12), but it seems that the blood must come into contact with collagen or other materials which are deep in the vessel wall, because thrombosis is not seen unless there is extensive damage to the endothelium, with exposure of these materials.
Thrombosis can occur in the microcirculation in such conditions as severe polycythaemia (an abnormally high concentration of red cells in the blood) and sickle cell anaemia. This is a congenital condition in which there is an abnormal haemoglobin in the red cells; the cells become sickle-shaped and less flexible if the partial pressure of oxygen in the blood is reduced, as for example on going to a high altitude.
Certain veins in the calf muscles tend to become dilated with increasing age and are then particularly prone to thrombosis. This type of thrombosis especially affects older patients who are undergoing surgery or are immobile in bed for long periods, as noted above. It is believed that sluggish blood flow in the dilated veins is a predisposing factor, particularly because it is found that measures which increase local blood velocity, such as exercising the legs or compressing them rhythmically (§14.5.2), protect against thrombosis. However, experimental studies suggest that increased coagulability of the blood also plays an important role, though it would not account for the preferential occurrence of the process in certain veins. Thrombosis may also occur in the left atrium of the heart, especially if this is dilated and there is atrial fibrillation (small irregular ineffective contractions of its muscle). It is suggested that the mechanism is similar to that in venous thrombosis, in that the blood flow in the atrium is sluggish.
It seems that thrombosis seldom occurs in less than two or three days in immobile patients, but may occur in an hour in a patient having surgery. However, if a vessel wall is damaged experimentally, platelets can be seen to aggregate within seconds at the site of damage. The rate of growth of the aggregate is then proportional to the local wall shear-rate. This is probably because platelets are carried to the site in greater numbers. In contrast, in the patients mentioned above, with venous and atrial thrombosis, wall shear-rates are apparently low at the sites of thrombosis. It is important to appreciate that there are also mechanisms operating in vivo to remove thrombi, so that there can be, for example, restoration of the patency of an obstructed vessel.
In normal circumstances the clotting of blood is not the only process, and probably not the most important one, involved in the arrest of bleeding when a vessel is cut. Indeed, patients with congenital absence of fibrinogen in their plasma may lead almost normal lives. It seems that the main factors involved in the immediate arrest of bleeding are actually the formation of a plug of aggregated platelets and constriction of the torn vessel. A clot then forms locally, adhering to the tissues and acting as a seal. As might be expected patients with a low blood concentration of platelets, or abnormal platelets, are liable to bleed spontaneously from small vessels and to bleed for prolonged periods from wounds.
We have seen that whole blood may be regarded, from a mechanical point of view, as consisting of flexible red cells suspended in a Newtonian fluid, the plasma. We now consider the sedimentation of red cells in blood, the principles of the measurement of blood viscosity and the viscous properties of blood.
In the discussion that follows it is assumed that the blood is studied in sufficiently large samples for the influence of the walls of the apparatus which confines it to be ignored, since this assumption simplifies the analysis. In practice, however, blood viscometry involves the use of small samples and the assumption is only partially valid.
10.6.1 Sedimentation of red cells. This topic is of interest because the sedimentation of red cells in blood can influence the mechanics of the circulation and may complicate the measurement of blood viscosity. Furthermore, observation of the rate of sedimentation of red cells in blood is an important diagnostic test.
In Chapter 5 (§5.2) we discussed the steady flow of a viscous fluid past a rigid spherical body immersed in the fluid, for the case when inertia is negligible. Such a flow occurs also when a rigid spherical particle sinks slowly through a viscous fluid and the walls of the vessel containing the fluid are sufficiently far away to exert no effect. In this situation the downward gravitational force of the particle is balanced by the viscous drag force. From this force balance the speed of fall (Uo) can be shown to be given by Stokes' law (Equation (6.1)), i.e.
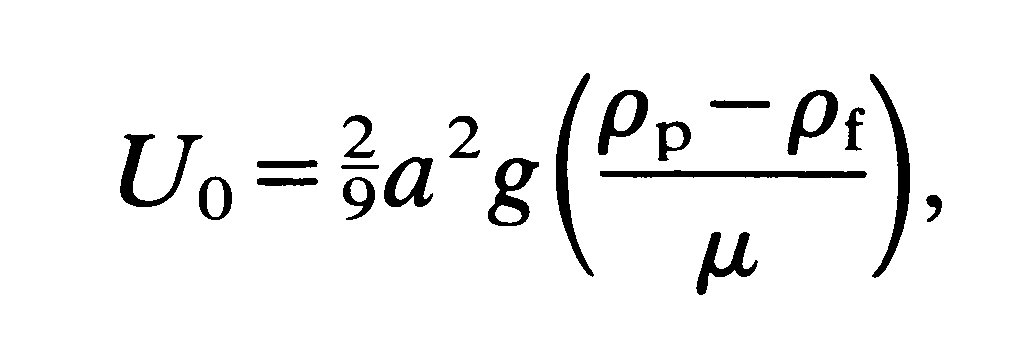
where a is the particle radius, rp, rf (rp > rf) are respectively particle and fluid density, m is fluid viscosity, and g is the gravitational acceleration. In particular we see that the sedimentation velocity of the particle depends on the square of the radius.
If the particle is released from rest in the fluid, its sedimentation velocity U increases until it attains the above steady value, which is called the terminal velocity (U0). Its velocity as a function of time t is given by
![]()
so that at large times (t >> T) U becomes equal to U0. The quantity T is a time scale for the process and is given by
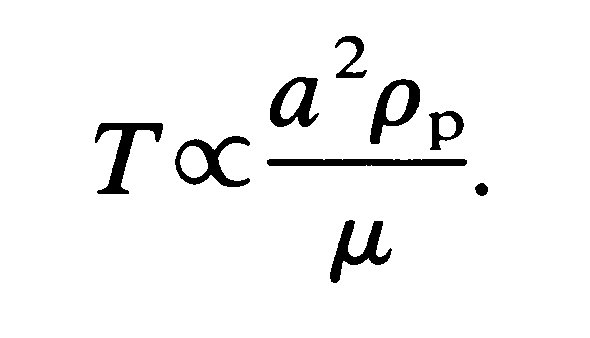
Thus it increases with particle size. Note that when t = 3T, U is approximately 95 per cent of U0 (Chapter 8, §8.3).
If we consider a rigid spherical particle the size of a red blood cell (8 mm in diameter) we find that T takes a value about 5 x 10-5 s. Therefore, the particle achieves a velocity which is 95 per cent of its terminal velocity in the astonishingly short time of about 10-4 s.
We cannot apply this theory exactly to a red cell, because of its shape and flexibility; nevertheless the theory for rigid spheres gives some indication of the behaviour of a single sedimenting red cell. At the moment no theory is available to describe the sedimentation of many red cells in suspension but the rigid sphere theory gives some feel for this problem also. If whole blood, which has been prevented from clotting, stands in a vertical tube the cells aggregate into rouleaux and then settle slowly, leaving clear plasma above. The distance moved by the upper boundary of the blood cells in the first hour is used as a laboratory screening test, called the erythrocyte sedimentation rate or ESR. The normal value for this test is about 3 mm s-1, conventionally reported as 10 mm h-1. In fact the sedimentation velocity is not constant, because there is initially formation of aggregates as noted above and the velocity falls as the cells begin to pack at the bottom of the tube.
In disease the ESR may be increased as much as tenfold, and this increase is associated with a raised concentration of fibrinogen and/or globulins in the plasma. These plasma proteins increase the tendency for red cells to form rouleaux (§10.3.2) and it is presumably the rapid sedimentation of these aggregates which accounts for the raised ESR. The change is not due to an alteration in the viscosity of the plasma, which is actually increased, and would thus reduce the ESR if it acted alone.
Under certain conditions, with blood flowing in a horizontal tube, the cells have been seen to sediment away from the uppermost surface and to pack more densely near the lowest surface, thus altering conditions at these interfaces. For example, the viscosity will be reduced near the top of the tube and raised at the bottom. This can presumably happen in vivo, if the blood flow-rate is very low, or there is a change in the plasma proteins leading to increased rouleaux formation.
The sedimentation of red cells could give rise to errors in the measurement of blood viscosity, particularly with a cone and plate viscometer (§10.6.2) which has practically horizontal surfaces. When operated at the lowest shear-rates red cells will tend to aggregate and sediment away from the upper plate towards the lower. This problem does not appear to have been studied in detail.
10.6.2 Principles of measurement of blood viscosity. Before proceeding to a discussion of the mechanics of whole blood in a shear flow we must first consider technical problems associated with the measurement of the viscosity of blood. These arise because it is a particulate suspension and may have non-Newtonian behaviour at physiological rates of shear.
If a material is suspected of showing non-Newtonian behaviour then its viscosity must be measured at a number of different shear-rates. In other words the rate of shear must be determined or vice versa. However, this is particularly difficult in non-Newtonian materials, because a viscometer which will give an essentially constant rate of shear throughout a sample of a Newtonian material may not do so in a sample of a non-Newtonian material. As we have seen, it is the presence of red cells which make normal blood non-Newtonian. The technical difficulties they introduce in viscometry are mainly associated with the fact that blood is not a homogeneous fluid. Thus the viscosity of blood will depend on the size of the sample that is studied; particular problems arise if the dimensions of the sample sheared in the viscometer are comparable with those of a red cell, or, if rouleaux form, with their size. This topic is discussed in detail in the chapter on the microcirculation (Chapter 13). No viscometer is perfect but some overcome these difficulties better than others.
Two types of viscometer are commonly used, namely capillary and rotational viscometers. In the first the fluid is made to flow along a tube of precisely known dimensions, by applying a given pressure difference between the ends. The instrument is constructed so that with a suitable choice of fluid the flow is laminar and effectively fully developed. The apparent viscosity of the fluid can then be obtained correctly from Poiseuille's law (§5.1).
A capillary viscometer is well suited to studying Newtonian fluids such as plasma, but is unsuitable for non-Newtonian fluids, including blood, for both the reasons already mentioned. The fluid is subjected to a wide range of shear stresses, varying from a maximum at the wall to zero at the centre line (§5.1). Secondly, because a small bore tube (say 100 mm diameter) has to be used to obtain a reasonable pressure difference with a fully developed laminar flow, the diameter of the tube is only a few times greater than that of the red cells (or of rouleaux). Under these circumstances the apparent viscosity of blood depends on the tube diameter, as discussed later (§13.5.1).
There are two types of rotational viscometer in common use, the concentric cylinder (Fig. 10.13)
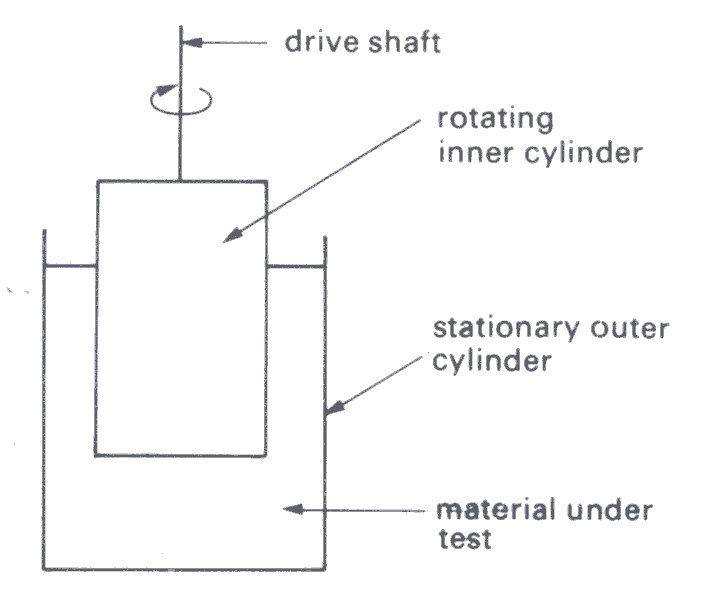
Fig. 10.13. Diagram of a concentric cylinder viscometer. (From Van Wazer, Lyons, Kirn, and Colwell (1963). Viscosity and flow measurement, p. 50. Interscience Publishers, New York.)
and the cone and plate (Fig. 10.14).
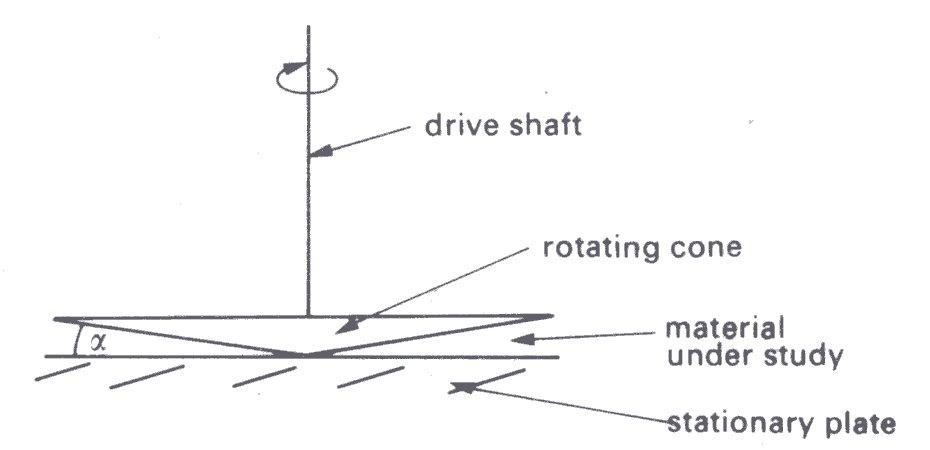
Fig. 10.14. Diagram of a cone and plate viscometer. a is the angle vetween the cone and plate. (After Van Wazer, Lyons, Kim, and Colwell (1963). Viscosity and flow measurement, p. 52. Interscience Publishers, New York.)
Both consist essentially of two parts, one of which is made to rotate at constant velocity relative to the other, separated by the material under test. Therefore torque is transmitted to the stationary part by the viscous action of the fluid. This can be measured by the angular displacement of the stationary part, if it is suspended from a wire; it will turn until the torsional force in the wire balances the frictional torque.
Both these instruments have advantages over the capillary viscometer for the study of blood, chiefly because the sample is mostly sheared at something approaching a constant rate if the design of the instrument is correct and the shear stress is sufficiently high. Both instruments also permit the study of a sample over an extended period of time, and of any time-dependent behaviour.
In a given concentric-cylinder viscometer, when there is a steady laminar flow of a Newtonian fluid in the gap, the shear-rate in the fluid is proportional to the imposed angular velocity and falls across the gap with the square of the radius (Fig. 10.15).
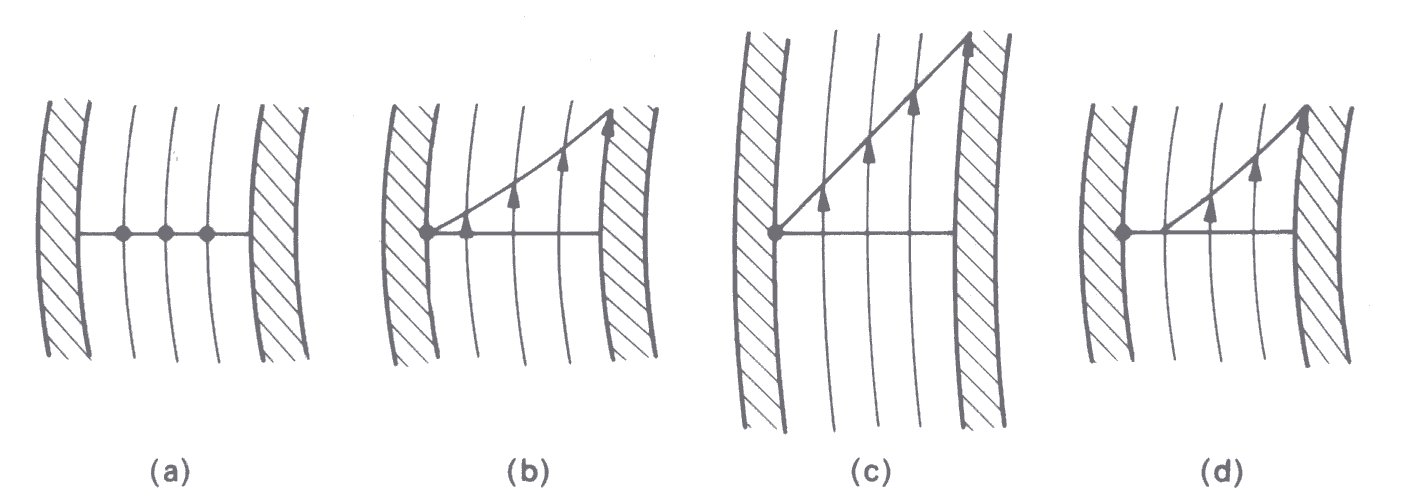
Fig. 10.15. Fluid velocity in streamlines in the gap of a concentric-cylinder viscometer. The inner cylinder rotates and the outer is stationary, (a) Apparatus at rest; (b) sheared Newtonian fluid—note that fluid velocity falls across the gap (see text); (c) if the gap width is very small compared with the radius of the cylinder, the velocity gradient is almost constant as between parallel plates (Fig. 10.1); (d) fluid with a yield stress. (After Van Wazer, Lyons, Kim, and Colwell (1963). Viscosity and flow measurement, p. 75. Interscience Publishers, New York.)
Therefore the shear-rate can be regarded as constant only if the gap width is much less than the radius. The torque transmitted to the outer cylinder by rotation of the inner (it is conventional to rotate the inner cylinder) is directly proportional to the shear stress and hence to the apparent viscosity of the fluid and the angular velocity.
If the material under study is non-Newtonian, neither the shear stress nor the measured torque is directly proportional to the angular velocity. Equations have been derived for the behaviour of different kinds of non-Newtonian material, but because these are based on highly idealized models of the materials, it is more appropriate to obtain the apparent viscosity of such materials by calibrating the viscometer with a Newtonian fluid of known viscosity. The test material is then examined at different rates of shear and it will be found that its apparent viscosity is shear-rate dependent. Further difficulty is experienced if the material exhibits a yield stress, since certain parts of the material do not flow when the shear stress is sufficiently low. Normal blood behaves like this at extremely low shear stresses.
In the cone and plate viscometer (Fig. 10.14) the test material is contained in the space between a cone of large apex angle and a plate with a flat surface normal to the axis. The cone is usually rotated and the torque transmitted by the material to the plate is measured. This instrument has some advantages over the concentric-cylinder device. In particular, in addition to using a smaller volume of test material, it is so designed that for small angles between the cone and plate (a < 3°) the shear-rate for a Newtonian fluid may be considered constant for all radial position; this is nearly true even for a non-Newtonian fluid, if its viscosity is not highly shear dependent. As in the case of a concentric-cylinder viscometer, a non-Newtonian material is studied by calibrating the instrument with a Newtonian fluid of known viscosity. However, it may not be possible to ignore the particulate nature of a material such as blood, because of the narrow gap across which shearing takes place. Near the apex of the cone this may be comparable with the dimensions of the blood cells, or aggregates of them.
10.6.3 Viscous properties of blood. We now describe experimental results on the viscosity of blood, examining first the dependence on shear-rate. The results in Fig. 10.16,
Fig. 10.16. Variation of apparent viscosity of human blood with rate of shear. (After Whitmore (1968). Rheology of the circulation, p. 67. Pergamon Press, Oxford.)
which are based on several studies with human blood, show the variation of the apparent viscosity with rate of shear. When the shear rate is about 1000 s-1, which is typical for many blood vessels in vivo (§13.1), the non-Newtonian behaviour becomes insignificant, and the apparent viscosity approaches an asymptotic value, which is in the range 3-4 mN s m-2. However, with reduction of the shear-rate the apparent viscosity increases slowly, until at a shear-rate less than 1 s-1 it rises extremely steeply.
In order to interpret these findings, we first consider the behaviour of blood at very low rates of shear. Rouleaux are known to form in blood at low rates of shear and a tangled network of aggregated red cells can be observed when blood is not sheared. If such blood is subjected to a shear stress below a critical value, the aggregated cell structure is believed to deform, without the blood flowing, that is, it exhibits a yield stress. There is certain experimental evidence which supports this idea: careful measurements with normal human blood show a yield stress of about 1.5-5.0 mN m-2. This decreases as the haematocrit is decreased, and there is a critical haematocrit below which no yield stress is found, as seen in Fig. 10.17.
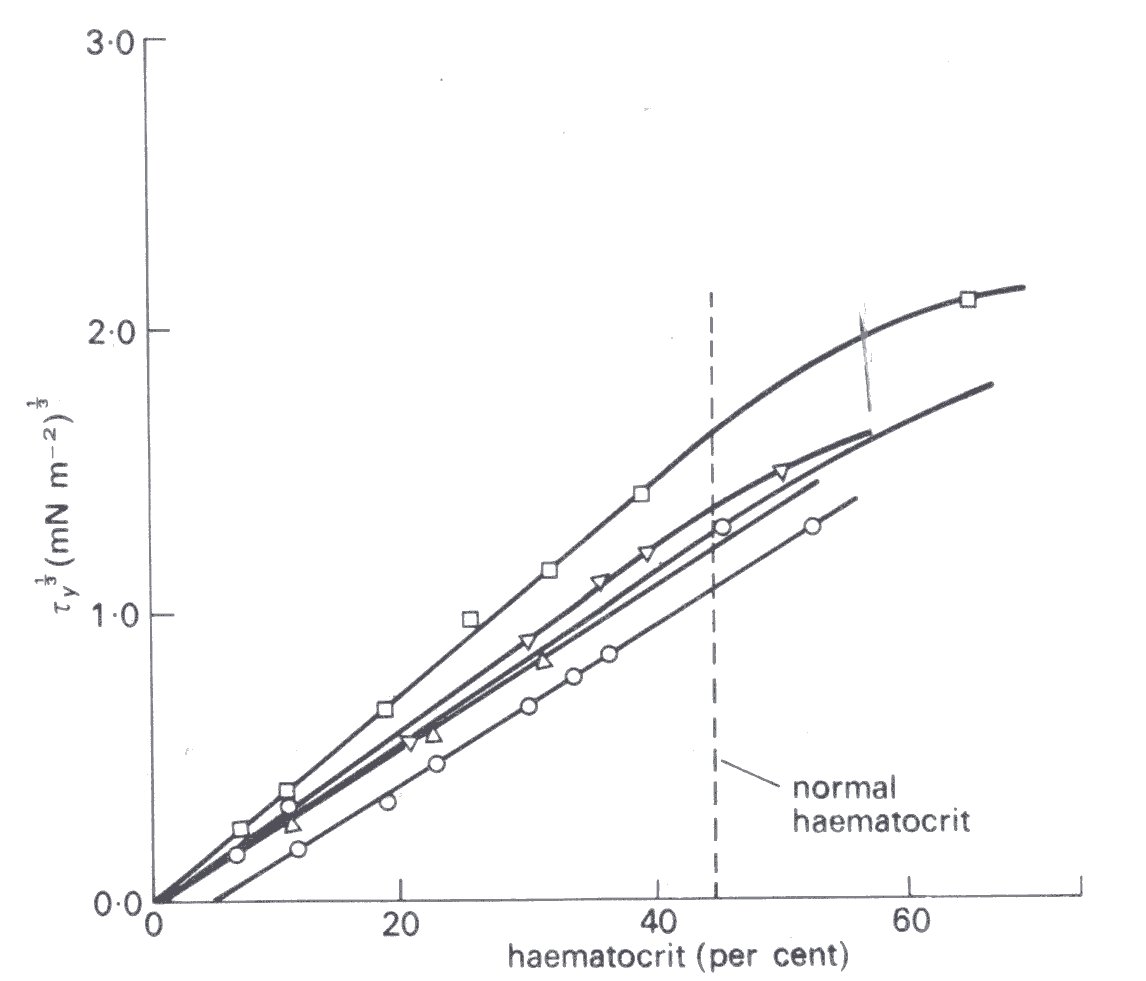
Fig. 10.17. Variation of yield stress (ty) of blood with haematocrit (5 different blood samples). When the haematocrit is less than about 5 per cent no yield stress is found. The haematocrit is plotted against the cube root of the shear stress, because of the observed linear relationship. (After Merrill, Gilliland, Cokelet, Shin, Britten, and Wells (1963). 'Rheology of human blood near and at zero flow'. Biophys. J. 3, 210.)
It is presumed that there are then too few red cells per unit volume of blood to permit complete bridging of the sample by a structure of aggregated red cells. The yield stress of blood is increased if the concentration of fibrinogen or gamma globulin in the blood is high, which is expected, because of the tendency for these asymmetric protein molecules to promote rouleaux formation.
The effect of the haematocrit on the mechanics of blood flow has been examined over a wide range of shear-rates, and behaviour at shear-rates up to 700 s-1 is illustrated in Fig. 10.18,
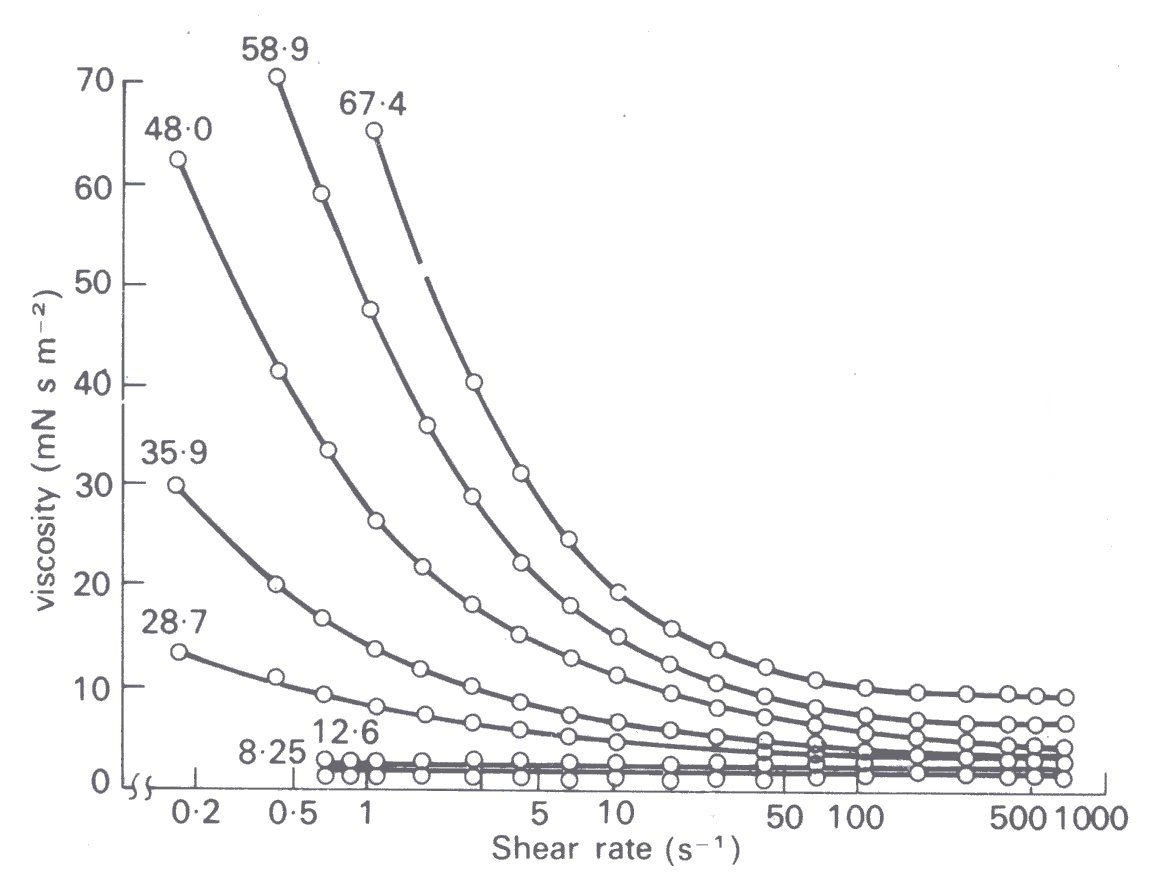
Fig. 10.18. Relationship between viscosity and rate of shear for human blood cell suspended in their own anticoagulated plasma at 25 °C for various stated volume concentrations of the erythrocytes. (From Brooks, Goodwin, and Seaman (1970). 'Interactions among erythrocytes under shear' J. appl. Physiol. 28, 174.)
Suspensions of red cells in plasma at haematocrits up to about 12 per cent are found to be Newtonian at all rates of shear, although they have a higher viscosity than plasma. However, as the haematocrit is further raised, i^ot only does the viscosity of the suspension increase, but non-Newtonian behaviour is observed, detectable first at very low rates of shear. We have already seen, in discussing the behaviour of suspensions (§10.1.1), the reasons for this increase of viscosity with haematocrit. The non-Newtonian behaviour of blood at very low rates of shear is partially due to the behaviour of the rouleaux. It has been observed microscopically, with a transparent cone and plate viscometer, that the average length of the rouleaux in blood decreases as the rate of shear is increased until the red cells are present individually and such a change can be expected to be associated with a reduction of viscosity (§10.1.2). In this context we should mention that rouleaux in a sheared flow have been seen to bend and straighten alternately as they rotate and that too can be expected to reduce dissipation (§10.1.2). These are not the complete answer, however, because a suspension of red cells in saline also exhibits non-Newtonian behaviour, and red cells in saline do not form rouleaux.
We must conclude, therefore, that the individual red cells are in part responsible for the non-Newtonian behaviour of blood. We have already noted that liquid droplets in a sheared suspension deform. There is experimental evidence, obtained with dilute suspensions of red cells, which indicates that they too deform when in a sheared flow (§10.3.2). Thus it seems likely that it is this deformation and rotation of the red cells which contribute to the non-Newtonian behaviour of blood. Strong support for this argument comes from a study with experimentally hardened red cells; a suspension of such cells in saline, even at a haematocrit of 40 per cent, is approximately Newtonian, like a suspension of rigid spheres (§10.1.1).
These observations suggest that the flexibility of the red cells plays an important part in determining the viscosity of blood and that at a given haematocrit and shear-rate the viscosity of a suspension of hardened cells will exceed that of normal cells. In general this expectation is borne out, as shown in Fig. 10.19;
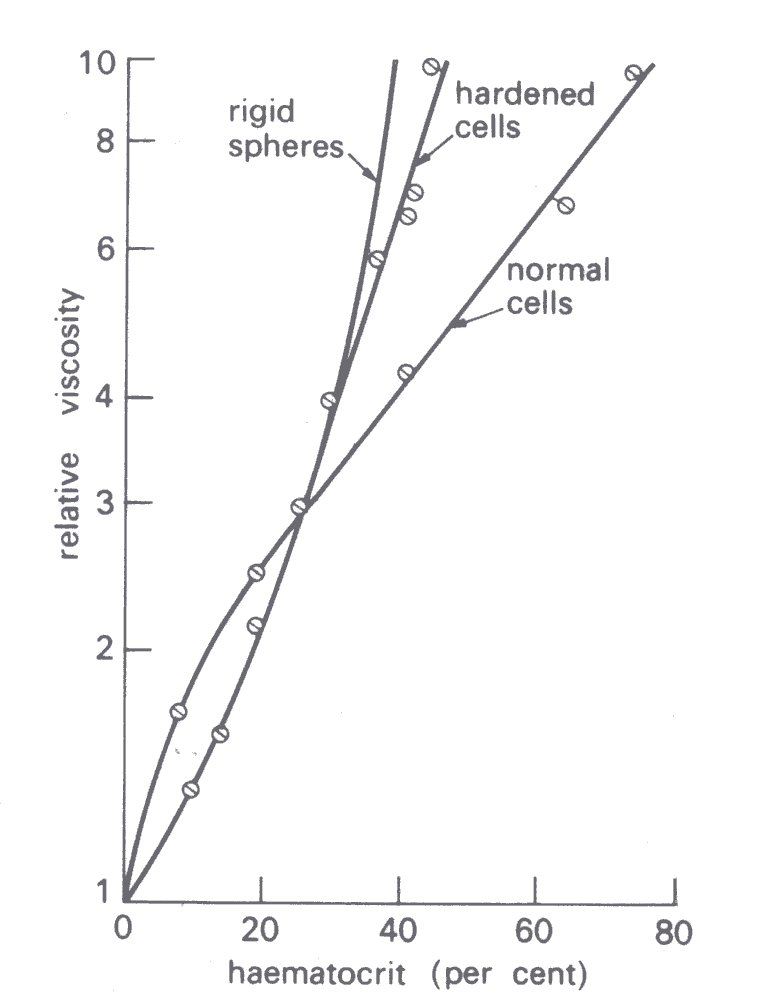
Fig. 10.19. Influence of haematocrit on the relative viscosity of normal and hardened cells suspended in saline (rate of shear 230 s-1). (After Whitmore (1968). Rheology of the circulation, p. 81. Pergamon Press, Oxford.)
at a haematocrit exceeding 30 per cent and a shear-rate of 230 s-1 the viscosity of a suspension of experimentally hardened red cells considerably exceeds that of a suspension of normal cells and approaches that of a suspension of rigid spheres. Similar findings are obtained, moreover, with red cells that have been sphered and are therefore less flexible (§10.3.2), and with the stiffer cells of patients with sickle cell anaemia (§10.6). It is a striking fact that the viscosity of a suspension of rigid spheres tends to infinity as the volume concentration (equivalent to the haematocrit) approaches 60 per cent, that is, it cannot be sheared. A suspension of normal red cells on the other hand will flow even at a haematocrit of 98 per cent!