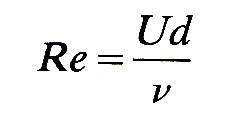
This chapter deals with the mechanisms of flow in the larger systemic arteries. The pulmonary arteries are specifically excluded, because they have special properties and are dealt with separately; thus we are concerned here with the aorta and its branches, which supply oxygenated blood to the organs of the body. As in other parts of the book, we take the vascular system of the dog as our primary example because it has been so widely studied experimentally; but we will refer to the situation in the human wherever specific differences of function or structure appear important. Again, we do not deal with active physiological processes such as reflexes, or mechanisms of vasoconstriction which may alter the flow or distribution of blood, but concentrate upon the physical properties of the system which are changed when such processes act.
This book deals with the arterial part of the systemic circulation in two parts—the arteries in this chapter, and the microcirculation in Chapter 13. First, therefore, we must describe how and why this subdivision is made, and then we shall provide a brief description of the anatomy and structure of systemic arteries, and of pressures and flows which occur within them. Thereafter we shall introduce the fundamental mechanics which govern events and then successively add the complicating or modifying features which bring us nearer to a complete description of the pressure and flow in the arteries; in doing this, we shall repeatedly refer to the mechanics described earlier in the book.
Traditionally, physiologists have dealt with the systemic circulation in terms of large and small vessels, with a rather arbitrary separation at or about the level of small arteries or arterioles. As will be discussed in Chapter 13, this separation has been made for various reasons, both physiological and mechanical; but it is most convenient and sensible in this chapter to subdivide the circulation on the basis of a fundamental difference in fluid mechanical properties which exists between small and large vessels. This is the difference between flows dominated by inertia, and viscous flow in which fluid inertia is negligible, which have been discussed in Chapter 5. The relative importance of these properties in a flow is expressed through the Reynolds number Re, where
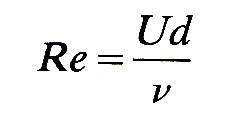
and is thus dependent upon the velocity U of the flow, the kinematic viscosity n of the fluid, and the diameter d of the vessel. We may recall from Chapter 5 that flows with Reynolds numbers much greater than unity will show the influence of inertia, whereas those with Re much less than unity will be dominated by viscous forces. In this chapter we shall deal with high Reynolds number flows in which the dominant forces are inertial. In practice, this means flow in the larger vessels (down to small arteries, approximately 100 mm in diameter, where Re falls below unity), because repeated branching causes a great increase in the cross-sectional area of the vascular 'bed' and thus the velocity of flow falls as the blood moves out into the smaller vessels.* [*Note that it is a reasonable assumption to regard blood viscosity as constant in these larger vessels, both because vessel diameters are large compared to individual cell diameters, so that blood can be considered a continuous fluid, and because shear-rates are high enough for viscosity to be independent of them (Chapter 10).] Chapter 13 covers the mechanics of small diameter vessels where viscosity dominates. It is important to recognize that the boundary between large and small Reynolds number flows may not be fixed in the circulation, because the Reynolds number depends on parameters which may vary widely; for example, increased flow through a particular vascular 'bed' - e.g. through a muscle during exercise—will occur through dilation of small vessels and an increase in blood flow velocity; thus the Reynolds number at any particular level will increase, and the boundary point will move outwards towards the capillaries. With vasoconstriction the opposite will happen.
12.1.1 The anatomy of large blood vessels. The anatomy of the canine aorta and its main branches is illustrated diagrammatically in Fig. 12.1, and many of the relevant dimensions are listed in Table I.
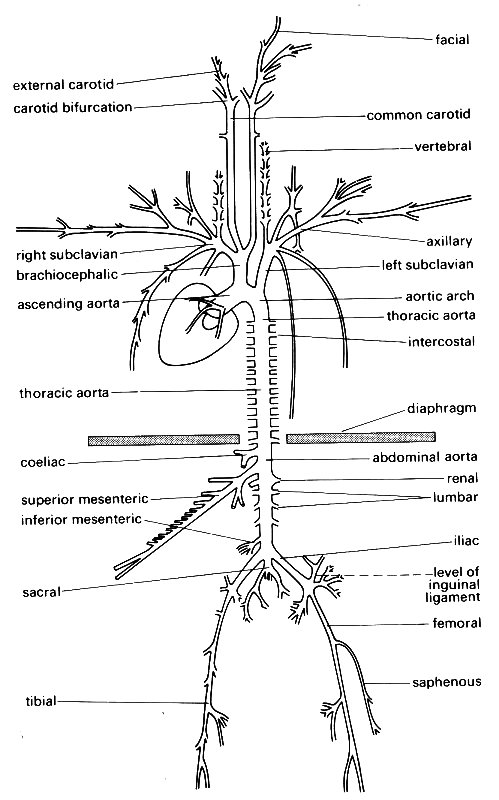
Fig. 12.1. A diagrammatic representation of the major branches of the canine arterial tree: (After McDonald (1974). Blood flow in arteries. Edward Arnold, London.)
The aorta takes origin from the left ventricle at the aortic valve, and almost immediately curves, in a complicated three-dimensional way, through about 180°, giving off branches to the heart, head, and upper limbs (Fig. 12.2);
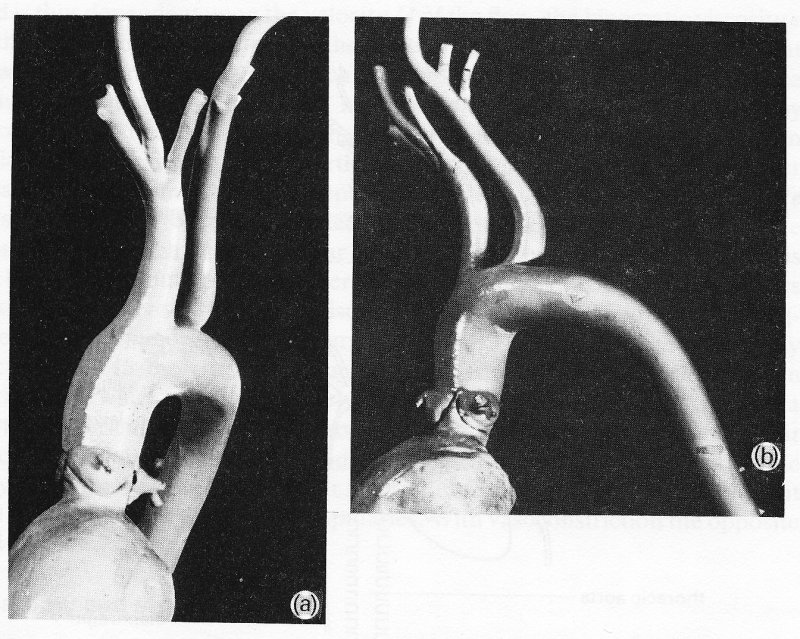
Fig. 12.2. Views from (a) the front and (b) the left side of a cast of the dog aorta, made at physiological pressure. Note the three sinuses of Valsalva and coronary arteries at the origin of the aorta. The Figure also illustrates the complicated curvature of the aorta in two planes, and the fact that the angles made by the brachiocephalic and left subclavian branches may be difficult to define, since the vessels go on curving after they leave the aorta.
it then pursues a fairly straight course down through the diaphragm to the abdomen, where it distributes branches to abdominal organs. Low down in the abdomen it terminates by dividing into the iliac vessels, which supply the hind limbs and (in the dog) the tail.
The aorta tapers along its length; the rate of tapering appears to be quite variable from animal to animal and probably from species to species; but in the dog, the area change fits quite well to an exponential equation of the form
![]()
where A is aortic area, A0 and R0 are the area and radius at the upstream site, x is the distance from that upstream site, and B is a 'taper factor', which has been found to lie between 0.02 and 0.05. This is quite marked tapering, as is shown in Fig. 12.3 (a),
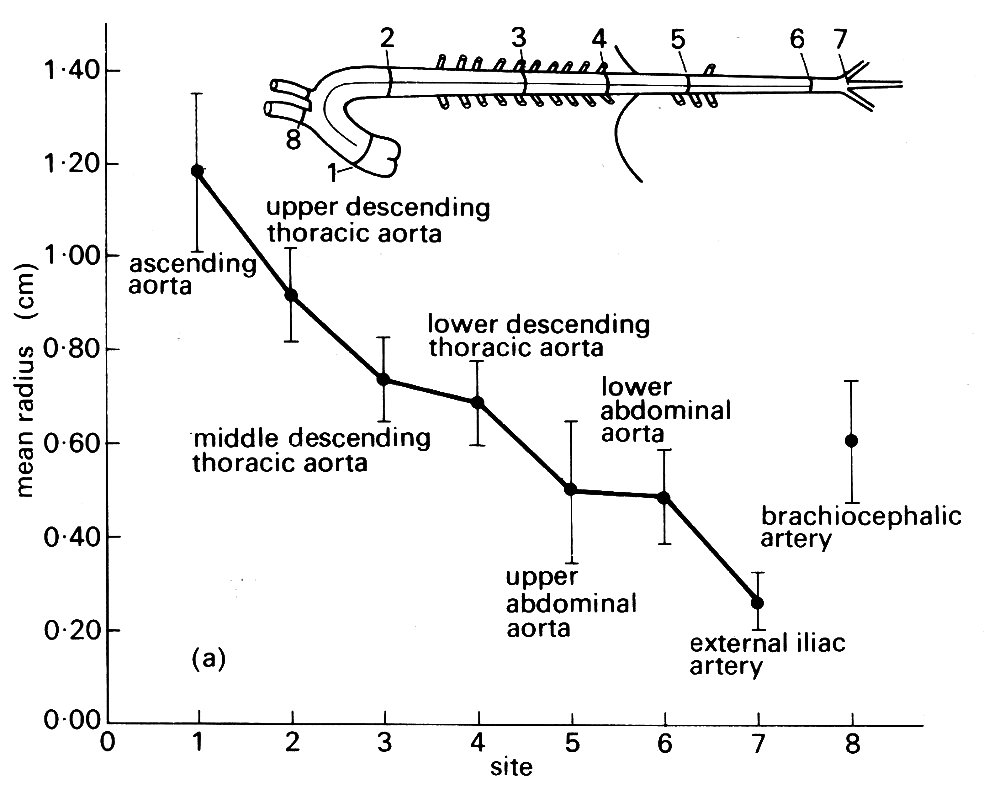
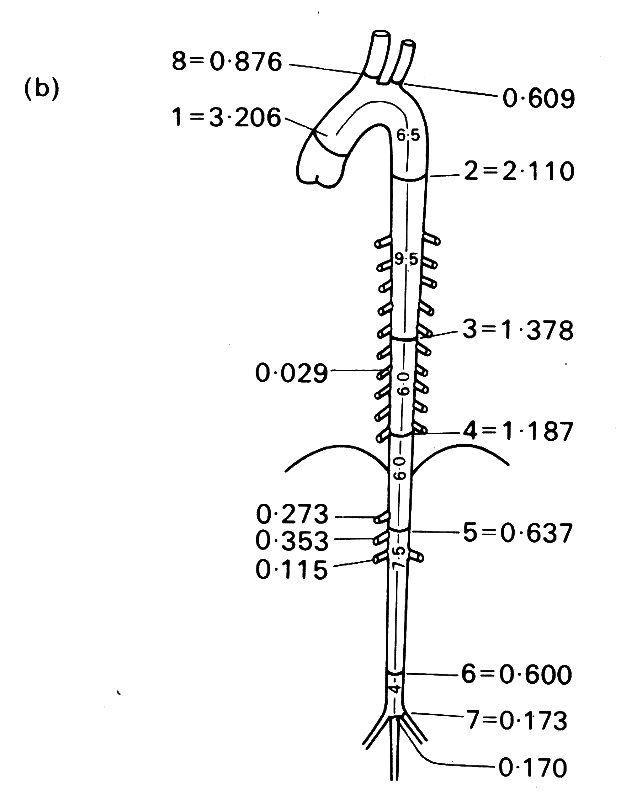
Fig. 12.3. (a) Taper in the aorta. The mean external radius of the aorta at various sites measured at physiological pressure in ten large dogs. (From Fry, Griggs Jr, and Greenfield Jr (1963). 'In Vivo studies of pulsatile blood flow'. In Pulsatile blood flow (ed. Attinger), p. 110. Used with permission of McGraw-Hill Book Company, New York.)
(b) Lumen cross-sectional area at various sites in the aorta and its main branches (details of data in (a)). (From Patel, de Freitas, Greenfield Jr, and Fry (1963). 'Relationship of radius to pressure along the aorta in living dogs'. J. appl. Physiol. 18, 111 1-17).
which is constructed from measurements of post-mortem canine aortic casts; the value of B corresponding to the taper in this figure is about 0.033. By contrast, the available evidence in man suggests that the tapering is not as smooth as this equation implies.
12.1.2 Branching ratios and angles. Although the aorta and other vessels taper individually, the total cross-sectional area of the arterial bed increases with distance from the heart. The data usually reproduced to support this statement are probably misleading for various reasons, including the fact that they were not always measured at physiological pressures, and there may have been some shrinkage resulting from the use of chemical fixatives. Measurements in living animals are of course difficult to obtain, and our knowledge is still incomplete, even for a single species. However, there is good information about the branches of the aorta in the dog, based on both direct measurements in living arteries and post-mortem casts made at physiological perfusion pressures. An 'average' aortic tree (based on such measurements in 10 fairly large dogs) is depicted in Fig. 12.3 (b).
In general the size of individual branches corresponds well to the amount of flow they conduct (the exception being the renal arteries, which are disproportionately narrow considering that they take 20-25 per cent of the cardiac output). However, if we calculate branching ratios (expressed as the sum of the areas of the daughter vessels at a branch divided by the area of the parent vessel, so that values greater than 1.0 imply an expansion of the vascular bed, and values less than 1.0 imply contraction), we find considerable variation, with values ranging between 0.79 and 1.29.
There is a tendency for the branches within the chest to have ratios close to 1.0, and for those in the upper abdomen to have slightly higher values showing expansion; but this is largely counteracted by contraction (ratio 0.85 - 0.90) at the termination of the abdominal aorta, and this is also found in man. Overall, there is little change; the summed areas of the branches of the aorta in Fig. 12.3 (b) are only about 7 per cent greater than that of the ascending aorta. Other experiments put this higher (up to 60 per cent expansion), the scatter reflecting the difficulties of accurately preserving physiological pressures throughout the vascular bed as the casting material sets.
However, there is no doubt that, beyond these early branches, the cross-sectional area of the arterial tree begins to expand dramatically. The most detailed study in the living state has been made in the bat's wing, wisich can be transilluminated and examined directly with a microscope. The results are summarized in Table 12.1. Everything except the capillary dimensions is, of course, scaled down, because even the aorta has a diameter of only about 1 mm in the bat, but the increase in total vascular cross-sectional area with branching is striking.
Table 12.1. Dimensions of blood vessels in the wing of the living bat |
|||||||
| Vessel | Average length (mm) | Average diameter (mm) | Average number of branches | Number of vessels | Total cross-sec area (mm2) | Capacity (mm3 x 10-3) | Per cent of capacity |
| Artery | 17.0 | 52.6 | 12.3 | 1 | 2263* | 38.4 | 10.1 |
| Small artery | 3.5 | 19.0 | 9.7 | 12.3 | 4144 | 14.4 | 3.8 |
| Arteriole | 0.95 | 7.0 | 4.6 | 119.3 | 5101 | 4.7 | 1.2 |
| Capillary | 0.23 | 3.7 | 3.1** | 548.7 | 6548 | 1.5 | 0.39 |
| Post-capillary venule | 0.21 | 7.3 | 1727.0 | 78233 | 16.4 | 4.3 | |
| Venule | 1.0 | 21.0 | 5.0 | 345.4 | 127995 | 127.9 | 33.7 |
| Small vein | 3.4 | 37.0 | 14.1 | 24.5 | 27885 | 94.7 | 25.0 |
| Vein | 16.6 | 76.2 | 24.5 | 1 | 4882 | 81.0 | 21.4 |
| *Average of individual
cross-sectional areas.
**Calculated. (From Wiedeman (1963). Circulation Res. 12, 376) |
|||||||
Comparable studies have not been carried out in other species, and in the dog information has to be pieced together from many sources, largely post-mortem preparations such as the casts mentioned above. The pattern which emerges is less precise, but very similar, and is illustrated in Fig. 12.4.
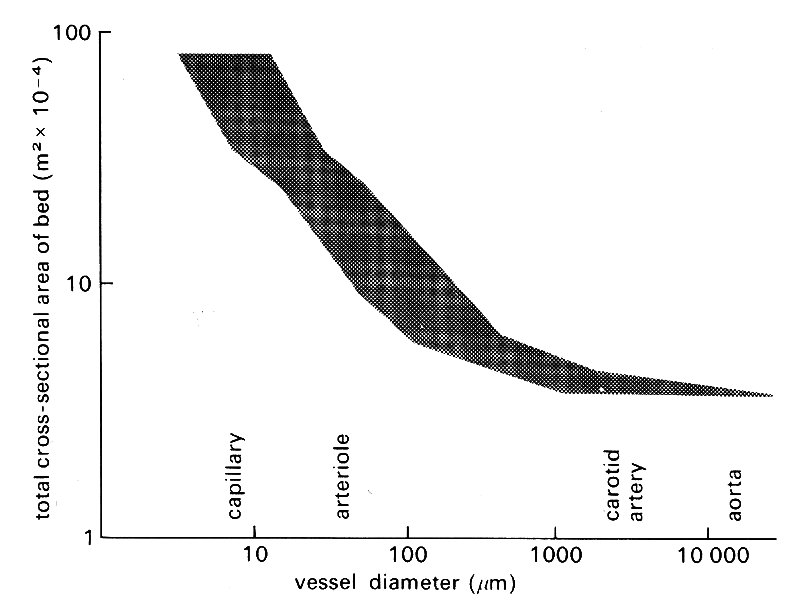
Fig. 12.4. Diagram illustrating how the cross-sectional area of the vascular bed expands peripherally. The scatter is not a consequence of experimental error; it reflects the fact that vessels at each level have varying diameters and degrees of taper. (Data from many sources, quoted by Iberall (1967). 'Anatomy and steady flow characteristics of the arterial system'. Math. Biosci. 1, 375-95.)
The same is true in man, where branching behaviour can also be studied in life, both by observation during surgery and by X-ray visualization of radio-opaque dye injected into vessels as a diagnostic procedure (arteriography). Fig. 12.5 shows the course and distribution of the carotid artery within the skull demonstrated in this way.
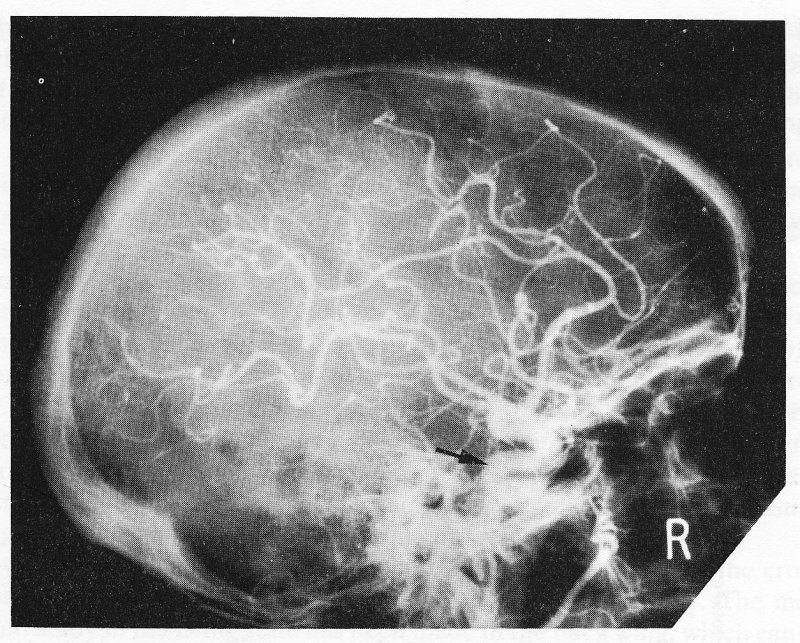
Fig. 12.5. A lateral X-ray of the skull immediately after injection of radio-opaque material into the carotid artery in the neck in man. The arrow shows the internal carotid artery, which follows a short, winding course within the skull and then divides into numerous branches which supply blood to the brain.
The angles at which branches come off the aorta vary just as do branching ratios, and it is clear that there is little symmetry in the structure of the central arterial tree, either in branching angles, ratios, or lengths; this must be borne in mind when we consider how to treat arterial behaviour quantitatively. Among the larger central arteries, symmetrical bifurcation is exceptional; in man the only example is the aortic bifurcation; in the dog, as Fig. 12.1 shows, there is none. Patterns of flow through arterial bifurcations are discussed in §12.8.2.
Further downstream, dichotomous branching with fairly narrow angles is commoner, though there are many exceptions and individual organs may have highly specialized arrangements not found elsewhere. In most organs, anastomoses, i.e. connecting links between different arterial branches, occur, or can develop to by-pass a blocked or damaged vessel. One of the most important of these lies at the base of the brain, where several vessels feed into a single ring, known as the Circle of Willis (named after the English physician who, in 1664, produced an authoritative account - with illustrations by Christopher Wren - of the anatomy of the nervous system); this in turn supplies branches to many parts of the brain.
12.1.3 The structure of the arterial wall. All arteries (and indeed veins - see §14.1) show a common pattern of organization, and are made up of similar materials, though the proportions vary in different parts of the circulation. We will first review the microscopic structure of the artery wall, and then discuss the functional importance of the various wall-layers and components, and some of the effects of ageing.
The arterial wall is made up of three layers: an internal tunica intima, surrounded by a tunica media, and then an external tunica adventitia. Each of these layers has a predominant structure and cell-type; the important features are illustrated in the examples in Fig. 12.6, which shows photomicrographs of transverse sections of a typical small artery.
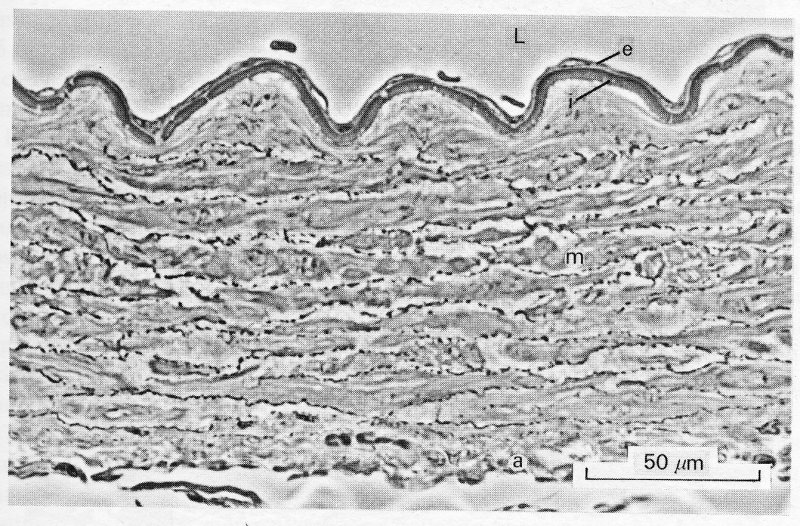
Fig. 12.6. (a) Abdominal aorta of the guinea-pig. Phase contrast photomicrograph of a section cut transverse to the long axis of the vessel. The full thickness of a small segment of the wall is shown. L:lumen e:endothelium i:internal elastic lamina m:media a:adventitia. This is a fairly typical 'muscular' artery. The lamellar structure of the media is well shown, with layers of smooth-muscle cells separated by darker, thinner bands of collagen and elastic fibres.
The tunica intima has two components. The innermost, which is in contact with the blood, is the endothelium; this is a single layer of cells, which extends as a continuous lining right through the circulation, covering all the surfaces which come in contact with the blood—arteries, capillaries, veins, heart-valves, and endocardial surfaces. It is mechanically rather fragile (being damaged by high shear-stresses, for example) but has considerable powers of regeneration and growth; it regenerates itself continuously, and can grow to form a lining over living or synthetic graft materials inserted surgically. The detailed structure of endothelial cells is dealt with in Chapter 13. Surrounding the endothelium is a thin subendothelial layer, containing a few collagen-generating cells (fibroblasts) and collagen fibres. Then comes a layer of branching elastic fibres - the internal elastic lamina - which is particularly well defined in smaller arteries (see Fig. 12.6 (a)) and forms the inner boundary of the next wall-layer, the tunica media. The tunica media is usually the thickest layer in the wall, and the one which shows the greatest variation in structure and properties in different regions of the circulation. Because of the differences occurring in this layer, arteries are generally divided into elastic and muscular vessels. This is an oversimplification, because there is no sharp subdivision, and there are also specialized variations in particular organs and species, but it does draw attention to the change in structure which occurs with distance away from the heart. The tunica media of large central arteries (the aorta and its large branches within the chest) is made up of multiple concentric layers of elastic tissue separated by thin layers of connective tissue, collagen fibres, and sparse smooth muscle cells which obliquely cross-link successive elastic layers. Smooth muscle cells are long (25-50 mm) and thin (5 mm), often with tentacle-like extensions, and contain contractile filaments of muscle which have the same basic form as those described in the muscle cells of the heart (§11.3.1). Under the microscope, these myofibrils are less prominent than they are in heart muscle cells because they are less systematically arranged and fewer in number, but their function is identical - they contract in response to depolarization of the cell-membrane, and generate tension. In large arteries, they tend to be orientated obliquely or longitudinally; in smaller, more peripheral arteries they lie increasingly more circumferentially, forming flat spirals.
The layered or 'lamellar' structure of the tunica media appears to be common to the large arteries of all mammalian species. In the aorta, where it has been studied in detail, the lamellae have a fairly constant thickness of about 15 mm, so that the total number present is closely proportional to the radius of the vessel both between and within species; thus the mouse aorta has five lamellae, the pig aorta over seventy.
Further away from the heart, the structure of the media changes, and the vessels are known as the muscular arteries, with the media consisting largely of spirally arranged smooth muscle cells (Fig. 12.6).
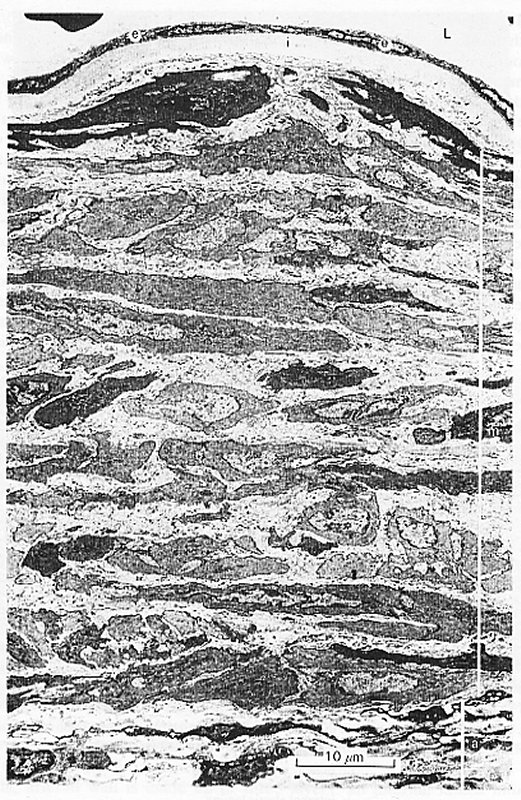
Fig. 12.6. (b) Transmission electron photomicrograph of the same specimen as in (a) at higher magnification. Note the single layer of endothelial cells, and the pale connective tissue which surrounds the muscle cells of the media. At the bottom of the section, in the adventitia, a few dark-staining fibroblasts and bundles of collagen fibres are visible. Photomicrographs by courtesy of Dr. G. Gabella.
Again these are disposed in multiple layers, with small amounts of connective tissue, collagen, and elastic tissue between them, and the number of layers diminishes as vessel radius diminishes; in very small arteries and arterioles there may be only one or two such layers. Throughout the smaller arteries, however, the tunica media remains the predominant element in the vessel wall; its outer boundary is marked by a very thin layer of elastic tissue known as the external elastic lamina.
The outermost layer of the arterial wall, the tunica adventitia, may in some places be as thick as or even thicker than the media, but it is less prominent microscopically. This is because it is composed of loose connective tissue, containing relatively sparse elastin and collagen fibres running in a predominantly longitudinal direction, and it has an ill-defined edge as it merges into the surrounding tissues.
The walls of all arteries larger than about 1 mm in diameter have their own nutrient blood vessels, the vasa vasorum. These take origin either from the parent artery or from a neighbouring one and break up into a capillary network which supplies the adventitia and, in larger vessels, reaches in as far as the inner layers of the tunica media. The nourishment of the tunica intima and the innermost layers of the tunica media depends predominantly on transport of materials from the arterial lumen. Small lymphatic vessels, and fine nerve-fibres running to the smooth muscle cells, also ramify through the tunica adventitia.
It has been known for many years that the elastic properties of arteries are non-linear. They become markedly stiffer as they are stretched (as shown in Fig. 7.5, §7.2), and an explanation of this was given in §7.2. There is in addition a progressive increase in Young's modulus which takes place with distance from the heart. This may be due to a number of factors, including the changing proportions of collagen, elastin, and smooth muscle and their arrangement.
Elastin and collagen, both of which are made up of long chains of protein molecules, are present in fibrous lattices and sheets in the various layers of the artery wall. The physical properties of both these materials have already been described (§7.2), and will not be repeated here. It is nonetheless worth repeating that in large arteries there is a fairly clear relationship between their properties and the elastic behaviour of the whole artery wall. On the other hand, the precise influence of smooth muscle on the properties of the larger arteries has long been a matter of controversy. This is principally because most studies have been carried out on excised blood vessels, where the state of contraction of the smooth muscle ('vasomotor tone') is likely to differ from that in the animal. However, there remain considerable difficulties even if studies can be performed on intact arteries within the animal. This is because contraction of smooth muscle in the intact circulation so decreases the total cross-sectional area of the vascular bed by constricting small arteries that the blood pressure in the large arteries rises; thus any diameter reduction due to an active increase in wall-tension is masked. Recent work, in which these effects are separated, has demonstrated that the contraction of smooth muscle can, even in the largest arteries where it is relatively sparse, produce considerable change in wall tension and actually constrict the vessel.
In the aorta, these calibre changes are small. For example, if the nerves supplying the smooth muscle of the aortic wall are stimulated electrically (mean blood pressure being held constant), aortic diameter decreases by only about 5 per cent. Most stimuli in the normal animal would be less intense than this, and it seems unlikely that physiological variations in smooth muscle activity would ever change aortic calibre by more than this. In more peripheral (muscular) arteries, the effect of smooth muscle is greater; a similar experiment in the femoral artery, for example, produces a 20 per cent diameter reduction, and cutting the nerves which supply the smooth muscle causes the diameter to increase above its resting level by a similar proportion.
The way in which smooth muscle contraction affects the properties of an artery will depend upon the conditions of the experiment and the way in which the measurements are made. If, for example, the diameter of a vessel is held constant and the smooth muscle stimulated, the wall becomes stiffer, and the incremental elastic modulus increases. If, on the other hand, the diameter is not controlled, then smooth muscle activity will constrict the vessel, and the elastic modulus may go down, as explained earlier (§7.2). In the normal living animal smooth muscle contraction stiffens the walls of large arteries (unless the vessel is so stretched that the collagen in the wall is taking much of the load; since the elastic modulus of maximally active smooth muscle is less than that of collagen, smooth muscle contraction would have no effect in this situation).
As was mentioned earlier, smooth muscle cells in large arteries tend to be orientated obliquely or longitudinally, and the cells appear to connect to the elastic tissue, particularly the internal and external elastic laminae of the tunica media. Thus they alter the wall-tension partly by pulling on the elastic tissue, and partly by acting in parallel with it and collagen. Their oblique disposition and the fact that they have a limited ability to shorten (by a maximum of about 25 per cent of relaxed length) probably account for their relatively slight effect on the diameter of large arteries even when they are maximally activated. The ability of some vessels, including quite large muscular arteries, to go into 'spasm' when handled experimentally or injured is presumably also a property of smooth muscle. However, it has not yet been adequately explained, because the lumen of an artery in spasm may be virtually obliterated, rather than reduced by the 20-25 per cent which sympathetic stimulation can produce and which the shortening properties of smooth muscle would predict.
In summary, therefore, the effects of smooth muscle on the size and stiff ness of large arteries are probably relatively slight under normal circumstances, particularly in comparison with its effects in smaller arteries, where it is the main constituent of the wall, and the near-circumferential arrangement of the fibres means that they can greatly alter the vessel lumen. Its activity there controls both the local distribution of flow and the overall resistance to blood flow, aspects which are dealt with in Chapter 13.
Smooth muscle does, however, have appreciable effects on the dynamic properties of the large vessels, as we have seen in Chapter 7. The viscous properties of the artery (stress relaxation, creep, hysteresis) are primarily attributed to the presence of smooth muscle, and greatly complicate wall mechanics (§7.2). One further dynamic property of smooth muscle, the physiological significance of which is undetermined, is the 'myogenic response'. It is a property of smooth muscle cells that they depolarise (and therefore contract) if they are stretched. The time-course of this response is slow (too slow for it to modify wall-properties during a single heart-beat, for example), but there is no doubt that it can significantly modify the stress-strain properties of the vessel wall. Its physiological role is a matter of continuing debate.
12.1.4 Arterial wall thickness. The thickness of the artery wall varies considerably through the circulation, and representative values are given in Table I. The measurements show a good deal of scatter; in the case of the small vessels, this is not surprising, because there are considerable problems in holding the vessels at their normal luminal pressures and preventing distortion as they are prepared for study. A further difficulty, which affects large vessels as well as small ones, arises because the tunica adventitia may merge gradually into surrounding tissues so that it is difficult to decide where the artery wall ends. The microcirculation does not appear to have been studied in the dog, and the values for very small vessels in Table I have to be drawn from other species - small mammals such as cats, rats, and mice. This is probably unimportant, as surveys of small vessel dimensions in mammals of widely varying body size have shown them to be remarkably similar.
This is far from true, however, in large vessels, where wall-thickness varies dramatically with body size among the smaller mammals. Fig. 12.7
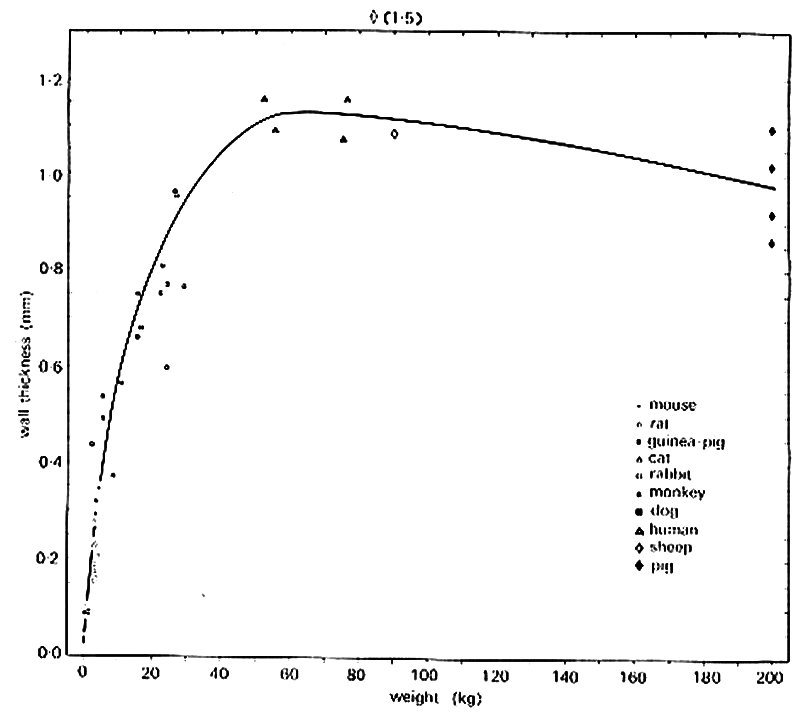
Fig. 12.7. Thickness of the media of the thoracic aorta in ten mammalian species. Medial thickness increases rapidly with adult body weight in the relatively small mammals; there is little or no increase with body weight in the large mammals. (From Wolinsky and Glagov (1967). Circulation Res. 20, 99.)
shows the results of a study of this, in which great care was taken to maintain the vessels at their in vivo size and to minimize and correct for distortion during histological preparation. Of course, diameter also varies greatly with body size in these large vessels; this is shown in Fig. 12.8,
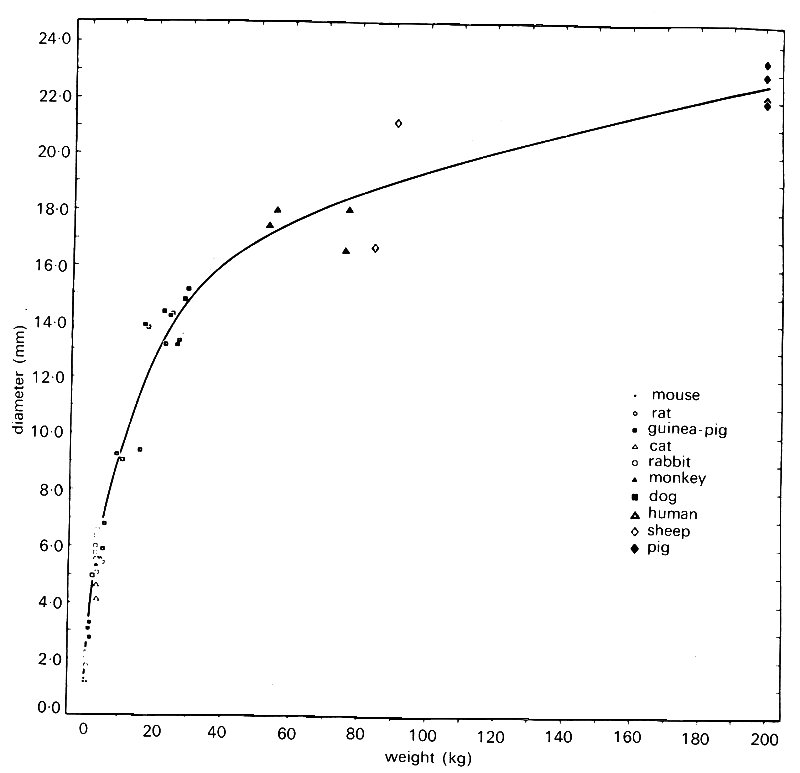
Fig. 12.8. Diameter of the thoracic aorta in ten mammalian species. Diameter increases more rapidly with adult body weight for small mammals than for large. (From Wolinsky and Glaeov (1967). Circulation Res. 20, 99.)
which is taken from the same source. As can be inferred from these two figures, the relationship between vessel diameter and wall-thickness, both within and between species, is approximately constant in large arteries; thus the h/d ratios in Table I are independent of body size.
In summary then, in large central arteries the internal diameter d and wall thickness h depend on body size, though the ratio between them (h/d) does not, and is thus independent of species and of site. As we move peripherally into small vessels, the walls become thinner, but h/d actually increases until in the very small arteries the external diameter may be almost twice that of the lumen even when the smooth muscle is relaxed. Finally, in the very smallest vessels in the microcirculation and particularly the capillaries, the relationship with body size disappears completely, and the diameter and wall-thickness are very similar in all mammalian species.
12.1.5 Changes in the arterial wall with age. The dimensions and properties of the larger arteries vary not only with body size and with position in the circulation, but also with the age of the animal. Systematic studies of the changes with growth and ageing have mainly been made in man, and many of the measurements have been made at unstretched length in post-mortem tissues, so that we know more about the histological changes with age than about precise dimensions. However, it is clear that the thickness and the structure of arterial walls are changing slowly throughout life, and these changes are reflected in the elastic properties. It is also clear that comparable changes occur in other species of mammals, though the evidence is less complete.
In the growing animal or child, both the diameter and wall-thickness of the large arteries increase steadily. Measurements at physiological degrees of stretch are lacking, and the values in Table 12.2 are for aortas at zero transmural pressure; h/d in these circumstances is virtually constant at all ages, an observation which has been confirmed repeatedly.
Table 12.2. Dimensions of unstretched arteries in man
|
|||
| Age (years) | Internal diameter d (mm) |
Wall thickness h (mm) |
h/d |
| 1 | 11 | 0.83 | 0.08 |
| 3-6 | 13 | 1.14-1.23 | 0.09 |
| 15-18 | 17 | 1.41-1.58 | 0.09 |
| 20 | 19 | 1.58 | 0.08 |
|
(Calculated from data from Dittmer and Grebe (1959), Handbook of circulation, p. 20. W. B. Saunders Company, Philadelphia.) |
|||
The increase in wall thickness in these central, elastic arteries is largely due to thickening and proliferation of the elastic lamellae in the tunica media, a process which is complete by early adult life, and thereafter merges imperceptibly into a different kind of histological change which is usually considered to be degenerative. Here, the elastic elements in the wall begin to fray and fragment, and may become calcified; the collagen fibres increase in number, both replacing muscle-cells and proliferating in other parts of the wall. The overall effect is that the diameter of the vessel increases, and its wall becomes thicker and much less distensible. This is 'hardening of the arteries', a process which affects large and medium sized arteries.* [*The term 'arteriosclerosis' is often applied to this process. However, confusion arises because this word is also sometimes used to describe the later stages of atheroma.] It is difficult to know whether to regard it as a physiological process or a disease state since it occurs universally, but shows a wide spectrum of severity. A more definitely pathological process, known as atheroma, may also occur. This is an increasingly common disease, which is now responsible for about half the deaths occurring in developed countries. Because of this, and because there has been a certain amount of investigation of the possible role of mechanics in its development, this is discussed in some detail in §12.9.2.
A number of studies have been made of the changes in dimensions and elastic properties which take place in human arteries with increasing age. Fig. 12.9,
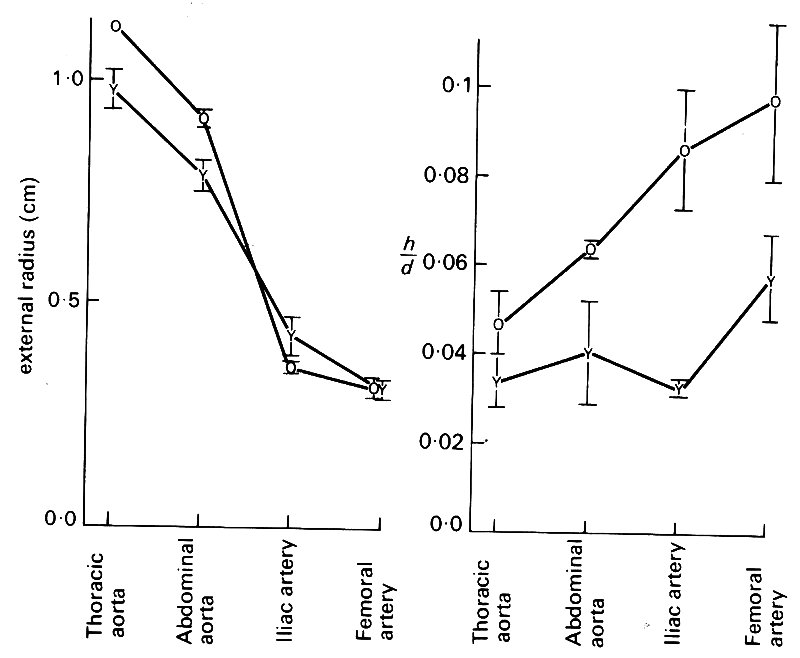
Fig. 12.9. The effect of ageing on radius and wall thickness of human arteries at physiological pressure. Average results from groups of young (Y) and old (0) arteries, plotted against position in the arterial tree. (From Learoyd and Taylor (1966). Circulation Res. 18, 278.)
which is taken from one such study, summarizes what takes place. Healthy arteries taken at post mortem from a group of 'young' (< 20 years) and 'old' (>35 years) patients were studied; they were held at their living length and inflated to physiological pressures. The aorta increases in diameter and thickens with age, the wall-thickness increasing slightly more than the diameter so that h/d is increased. The smaller, 'muscular' branches of the aorta do not change appreciably in diameter, though their walls thicken considerably. Thus old vessels dilate and thicken, but to different degrees at different sites; the big vessels tend to dilate and thicken, while the smaller ones show only wall-thickening.
Accompanying these changes in dimensions are interesting changes in elastic properties. In the thoracic aorta, at physiological pressure (1.33 x 104 N m-2, 100 mm Hg) the incremental Young's modulus E (§7.2) increases steadily with age (Fig. 12.10 (a));
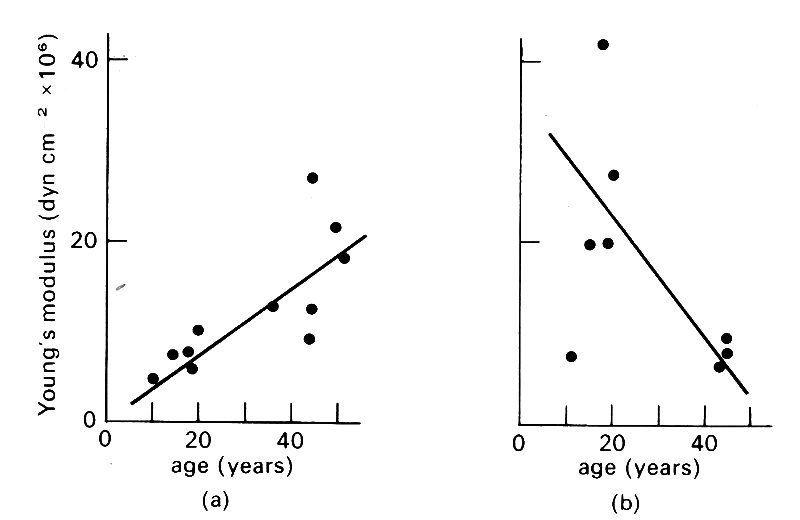
Fig. 12.10. Effect of ageing on elastic properties of arteries, (a) Incremental Young's modulus plotted against age for normal human aorta at a pressure of 100 mm Hg. (b) Similar data for iliac artery. (From Learoyd and Taylor (1966). Circulation Res. 18, 279.)
more peripherally, however, there is no change, or a fall (Fig. 12.10 (b)). The explanation of this appears to be that the diameter of the aorta increases with age; thus it is further along its (non-linear) length-tension curve, (Fig. 7.5 (a), §7.2) and E is correspondingly greater.
We can summarize a good deal of this section by saying that the dimensions and elastic properties of arteries vary greatly with age and body size as well as with their site in the circulation. Much of this is intuitively obvious - if we think of a mouse and an elephant we can all predict a correlation between aortic size and body weight, for example. Nonetheless a certain amount of detail is essential, because many of the properties are less obviously related, and in the rest of this chapter we shall be examining mechanical phenomena (such as pressure and flow wave-forms) which can only be clearly understood if the behaviour of the arterial wall and the anatomy of the vascular bed are known in some detail. Finally, this section has a cautionary value, since it concerns variability in biological systems. Physical scientists who study the circulation need quantitative information, and are often frustrated by the inability of physiologists to provide it. It may be salutary to illustrate that a simple parameter like aortic diameter not only is extremely difficult to measure, but will show variation with species, site, age, body size, blood pressure, and smooth-muscle activity. If we wish to calculate Reynolds number for the aorta, we need not only vessel diameter, but also two other measurements - blood velocity, and viscosity; to calculate pulse-wave velocity using the Moens-Korteweg equation (§12.3.4) we must have diameter, wall-thickness, density, and Young's modulus for the wall. Now all these measurements will, like aortic diameter, be subject to a number of biological influences, and will therefore show variation. It follows that derived parameters like Re may show wide variation even when they are calculated from accurate and compatible measurements. If they are calculated from badly chosen data, this variability will become grotesque.
The pressure in all systemic arteries fluctuates, the source of the fluctuations being the pumping action of the left ventricle. A typical aortic pressure record is shown in Fig. 12.15, and there are many other examples in this book. Certain conventions are followed in describing arterial blood pressures, and we need to examine these with some care in order to understand exactly what is meant, and how relevant the measurements are to the mechanics of flow.
The first convention is that of expressing the pressure in mm Hg. This unit does not appear in any international system, old or new, but arose because the blood pressure is actually measured in mm Hg in the vast majority of cases, using an inflated cuff connected to a mercury manometer to occlude the artery in a limb; this is known as a sphygmomanometer. In defence of the unit, it should perhaps be pointed out that it has been in continuous use since it was introduced (by Poiseuille) in 1828, and has therefore seen several other units come and go. In deference to its wide familiarity it is used widely in this book together with the corresponding SI unit.* [*1 mm Hg = 133.32 Nm-2.]
The second convention in expressing blood pressure is to refer it to atmospheric pressure. The assumption usually made is that this is equal to the pressure just outside the artery, so that the blood pressure is considered to be transmural pressure (transmural pressure is p1-p0, and here p1 is internal pressure and p0 atmospheric pressure).
12.2.1 Transmural pressures. We need to know what the transmural pressure is for a variety of reasons. We need it if we are to examine the force-balance between blood and wall, and if we are to choose realistic wall-properties for the living state when their measurement has to be made post mortem. It also tells us something about the load against which the heart must work, and about the state of the peripheral vascular bed, blood volume, reflex activity, and many other physiological events. It does not, however, tell us anything about the force which is being applied to cause motion of the blood—to know that we need the pressure difference between two points in the circulation, just as we need the pressure difference between inside and outside of the arterial wall in order to examine the forces acting across it. The point to be made here is that the pressures measured by a physiologist are often not those needed by an engineer for a physical description of the system. For example, the pressure difference across the wall of a large artery in a limb—the conventional 'blood pressure'-may be, on average 1.33 x 104 N m-2 (100 mm Hg); but the pressure difference between the ascending aorta and such an artery, which is the force which actually drives the flow between them, averages only about 0.03 x 104 N m-2 (2-3 mm Hg) and is rarely measured because it is technically extremely difficult to do so.
An important factor influencing transmural pressure is gravity. This is easiest to understand if we consider the situation in a dead animal. All the vascular smooth muscle relaxes, and the blood redistributes itself. The increase in volume of the peripheral vessels and small veins is so great that many large vessels are virtually emptied, and may collapse.* [*The term 'collapse' is defined in §7.3; it does not necessarily imply that the vessel is completely empty.] In the absence of gravity, the pressure would be the same, and practically equal to atmospheric, in all vessels.
We can understand the effect of gravity if we consider the dead body propped upright. The blood will now redistribute itself, and above a certain level in the body where the pressure is equal to atmospheric (the 'equal pressure point') all the vessels will be collapsed. From that level upwards, if the vessels are empty, the pressure in them will be equal to the surrounding tissue pressure, and hence approximately equal to atmospheric pressure pA. Below that level (and above it if the vessels there are not completely empty) the pressure in the vessels pi is given by
pi = pA + hrg (12.1)
where h is the vertical distance below the equal pressure point (h is negative above that point), r is the density of blood, and g the acceleration due to gravity. This equation is, of course, identical to Equation (4.2), §4.2, and the pressure we are considering is the hydrostatic pressure.
Hydrostatic pressure is an important force for the redistribution of blood in the living vascular system, as well as in the corpse. The zero level (h = 0) in a man standing upright is approximately at the level of the heart (Fig. 12.11);
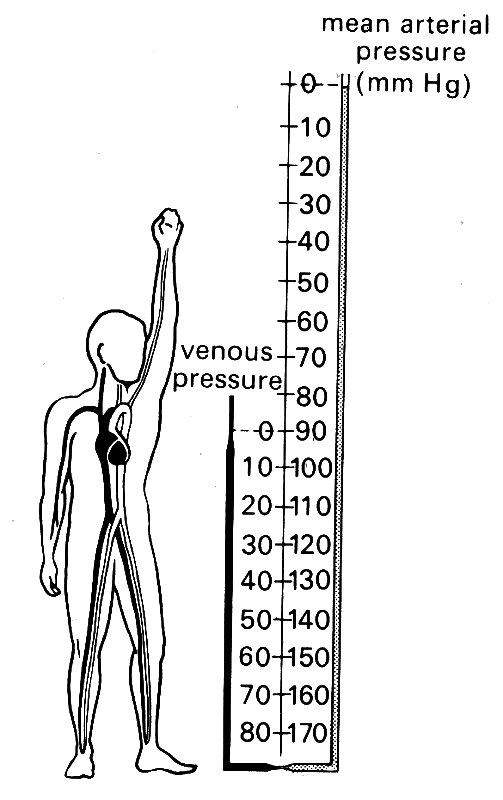
Fig. 12.11. Mean arterial and venous pressures in the human circulation, relative to atmospheric pressure. (After Rushmer (1970). Cardiovascular dynamics, p. 196. W. B. Saunders Company, Philadelphia.)
thus veins in the neck are normally collapsed (but not completely so; blood still flows through them) and the 'filling pressure' of the heart (Chapter 11) is close to atmospheric pressure. This filling pressure can be altered either by changes in blood volume, or by changes in the volume of the vascular bed in the lower limbs.
The most familiar expression of gravitational effects is fainting, where one of the important features is that when the subject stands up, the volume of blood in his leg veins increases abnormally, and the venous filling pressure of the heart falls. This leads to a fall in cardiac output and thus of blood supply to the brain. Falling or lying down relieves the faint by eliminating the force which is holding blood in the leg vessels. One of the reasons why everyone does not faint on standing is that reflex constriction of the veins in the legs normally occurs so that their ability to act as a reservoir is greatly reduced. Another reason is that there is arteriolar constriction which increases the resistance to flow so that arterial blood pressure does not fall significantly. If vasoconstriction is prevented (e.g. by certain drugs or diseases) fainting or dizziness on standing become common; and it also occurs where the vascular bed is greatly dilated as m hot climates or after a hot bath. The same mechanism may cause pilots' to black out when they execute 'high-g' turns in high performance aircraft if the tension generated in the vessel walls is not great enough to balance the hydrostatic pressure even with vasoconstriction. The vessel walls will then be stretched (becoming progressively stiffer, see Fig. 14.2, §14.2) until the tension within them does balance the pressure.
The quantitative relationship between the transmural pressure (pi-po) and wall-tension is expressed by the Law of Laplace (Equation (7.6)), which tells us that
T = (pi - p0)R
where T is the wall-tension per unit length of tube and R is the tube radius. As the transmural pressure and radius increase, a balance can only be struck if T increases more rapidly. Thus the stability of vessel walls depends upon their non-linear elastic properties. Note that in distending a vessel it is just as effective to lower p0 as to raise pi; a normal person can be made to faint if the lower half of his body is subjected to a subatmospheric pressure. Physiologically, the systemic vessels within the chest are subjected to a p0 which swings above and below atmospheric with each breath, and this has important consequences, particularly for the stability of veins (see Chapter 14).
From what has been said so far, it will be clear that the hydrostatic forces are an important component of the forces acting on vessel walls, particularly the veins. The situation in life is illustrated in Fig. 12.11, in which the mean arterial blood pressure (1.2 x 104 N m-2, 90 mm Hg) is added to the hydrostatic pressure acting in arteries, but not in veins. The transmural pressure in a leg artery may be four times that in the raised arm, while the arm veins will empty towards the heart and collapse when the arm is raised above the level of the chest.
Thus the transmural pressures encountered in the normal circulation can vary very considerably, a point which is often forgotten in calculations of the force balance on the arterial wall. Nor is the 'safety margin' in arterial pressure very great; as has been explained in Chapter 7 (§7.3), the artery may collapse whilst there is still a slightly positive (i.e. distending) transmural pressure. Here again is a source of biological variation; the standing giraffe has to have a much higher mean arterial blood pressure than man in order to prevent the collapse of the arteries supplying blood to the brain.
The effects of hydrostatic pressure on the. distension, and therefore elastic properties, of arteries and veins tend to be forgotten. This is because clinicians measure blood pressure in the upper arm, which is approximately at the upper chest level, where the hydrostatic component of the transmural pressure in a lying or standing patient is zero. In studies of the circulation where fluid-filled catheter and manometer systems are used, the convention is to align the manometer diaphragm at 'mid-chest' level, which also eliminates the hydrostatic pressure component. Thus the hydrostatic term in Equation (12.1) (hrg) is zero, and the 'excess pressure' generated by the heart is the only one described. It is worth remembering, when considering the elastic behaviour of arteries, that a transmural pressure of 200 mm Hg may be entirely normal in dependent limbs.
12.2.2 Unsteady pressure in large arteries. The rather complicated patterns of transmural pressure which may arise in the circulation are of interest from the point of view of vessel wall mechanics, but they should not be allowed to obscure the real nature of the pressure force which drives the flow. This has nothing to do with transmural pressure—flow can occur through an almost completely collapsed tube, as it does for example when blood returns through the neck veins to the heart in an upright subject. Nor is the hydrostatic pressure important; it requires the same amount of energy to force fluid through a tube whether it is horizontal or vertical (provided the size is unchanged). Thus when we consider the forces governing flow, we are exclusively interested in the pressure generated by the heart, which we shall call the excess pressure (pe). This quantity is the difference between the actual pressure and its hydrostatic component, and is commonly referred to as 'blood pressure'. It is the gradient of excess pressure which drives the flow. The distribution of excess pressure through the circulation is illustrated in Fig. 12.12;
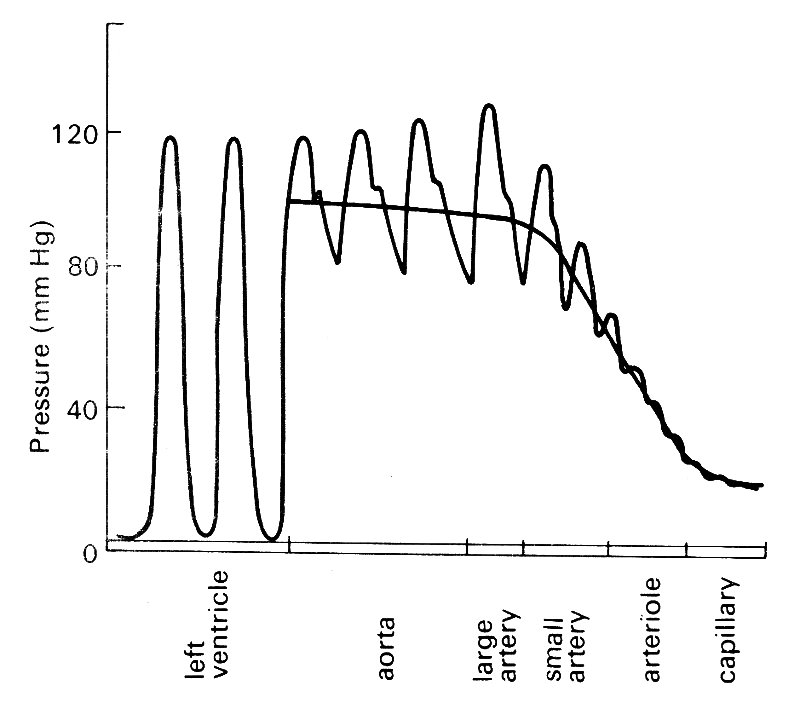
Fig. 12.12. Wave-forms of excess pressure, and its mean level, in the arterial circulation.
it can be seen that it is largely dissipated in forcing the blood through the microcirculation. That will be dealt with in Chapter 13; here we are interested in the much smaller pressure gradients necessary to force flow through the large arteries, and in the rest of this chapter we shall be concentrating on them, and on the flows which result. In many parts of this book we shall follow common practice and refer to the excess pressure as blood pressure, or simply pressure, since the meaning will be clear in context.
We will examine the pressures first. The pressures in the left ventricle and in the ascending aorta immediately downstream from the aortic valve are shown in Fig. 12.13.
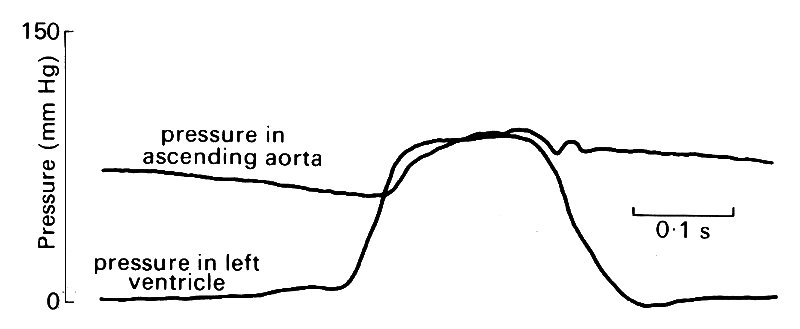
Fig. 12.13. Simultaneous recordings of pressure in the left ventricle and the ascending aorta of the dog. (From Noble (1968). 'The contribution of blood momentum to left ventricular ejection in the dog'. Circulation Res. 23, 663-70.)
These were recorded simultaneously, using a pair of extremely carefully matched pressure transducers, and are therefore a faithful record of events instantaneously during the cardiac cycle.* [*We shall see that it is the unsteadiness of pressure and flow which dominates the fluid mechanics of large arteries, and experimental apparatus must be capable of responding fast enough to register such changes faithfully. Thus, in addition to the usual requirements of stability and adequate sensitivity, is added that for a good frequency response. This is often a much more rigorous demand and has not always been adequately met in the past (see §12.2.5).]
As was described in Chapter 11, pressure rises rapidly in the ventricle at the beginning of systole, and soon exceeds that in the aorta so that the aortic valve opens, blood is ejected, and aortic pressure rises. During the early part of the ejection phase, ventricular pressure exceeds aortic pressure. About half way through ejection, the two pressure traces cross, and there is now an adverse pressure gradient across the aortic valve, which is maintained as both pressures start to fall. At this point there is a notch on the aortic pressure record (the dicrotic notch) which marks the closure of the aortic valve, and thereafter the ventricular pressure falls very rapidly as the heart muscle relaxes. The pressure in the aorta falls much more slowly. This fall is easy to understand if we remember that the large central arteries, and particularly the aorta, are elastic, and thus act as a reservoir during systole, storing some of the ejected blood which is then forced out into the peripheral vessels during diastole.
If we now move slightly downstream, and examine the pressures at two points on the axis of the aorta (e.g. points 0 and 4 cm in Fig. 12.14)
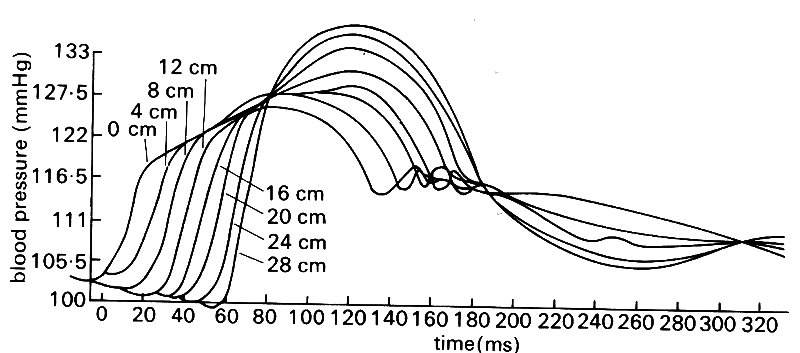
Fig. 12.14. Simultaneous blood pressure records made at a series of sites along the aorta in the dog: 0 cm is at the start of the descending aorta. (From Olson (1968). 'Aortic blood pressure and velocity as a function of time and position'. J. appl. Physiol. 24, 563-9.)
we can see that the pressure records are almost identical in shape at the two sites, but the one at the downstream point is slightly delayed. In other words, the pressure pulse generated by ventricular contraction is travelling along the aorta as a wave. We can roughly calculate its velocity from the delay if we know the distance between measuring sites, and we can also work out the pressure difference driving the flow along that segment if we subtract the downstream pressure from the upstream one.
If we make simultaneous measurements at points all along the aorta (or, as is technically much easier, make successive measurements at different sites with a catheter and align them by reference to the signals from a second, fixed, reference catheter) then we see that the pressure wave changes shape as it travels down the aorta (Fig. 12.14). It is progressively delayed, of course, but also steepens and increases in amplitude, whilst at the same time losing the sharp dicrotic notch. Thus we have the paradox that the systolic pressure actually increases with distance from the heart. (This is not a peculiarity of the species; it is also systematically observed in man and other animals.) In fact, of course, the mean level of the arterial pressure falls with distance from the heart; it is difficult to visualize this from the figure, because the fall is only about 0.05 x 104 N m-2 (4 mm Hg) along the length of the aorta, whilst the amplitude of the pressure oscillation between systole and diastole nearly doubles.
This process of amplification of the pressure pulse continues in the branches of the aorta out to the level (in the dog) of about the third generation of branches - for example, the saphenous artery in the lower leg, with an internal diameter of 1-2 mm (this is shown in Fig. 12.19). Thereafter both the oscillation and the mean pressure decrease rapidly to the levels found in the microeirculation.
The radial expansion and contraction of the arterial wall which takes place with the passage of the pressure wave has been measured by a number of methods. One such measurement is shown in Fig. 12.15,
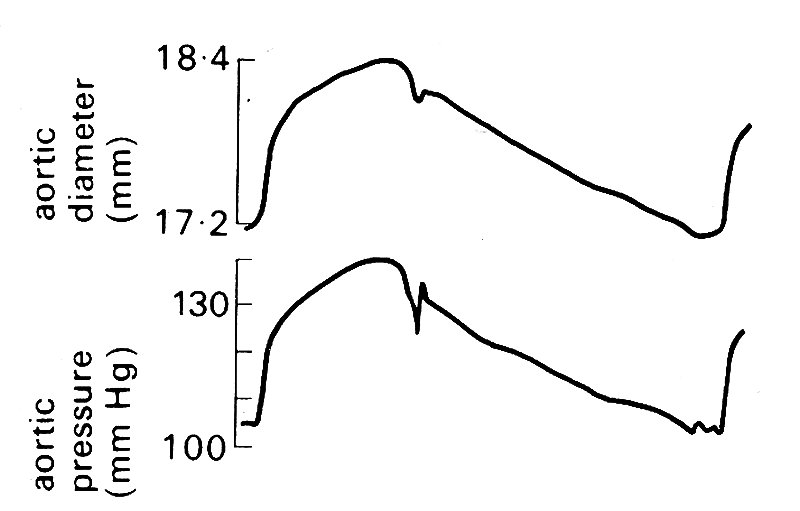
Fig. 12.15. Simultaneous records of aortic diameter and pressure during a single cardiac cycle in the dog. (From Barnett, Mallos, and Shapiro (1961). 'Relationships of aortic pressure and diameter in the dog'. J. appl. Physiol. 16, 545-8.)
together with the pressure within the vessel, recorded simultaneously. It can be seen that the motion of the wall is virtually in phase with the pressure; in other words, the wall behaves like a purely elastic material, with little evidence of hysteresis due to visco-elastic properties (see §7.2). Note also that the change in radius is small; expressed as a strain (§7.1) it is about 7 per cent. These observations justify the use of linear elastic theory to describe the behaviour of the arterial wall, expressing its properties in terms of a constant elastic modulus E (§7.2). As we shall see in the next section of this chapter, linear elastic theory works very well as a first approximation in describing the wave, and for predicting the wave speed.
12.2.3 Flow. In order to complete our description of events in large arteries, before going on to consider the detailed mechanics, we must examine the flow along the aorta and its branches. Predictably, since the pressures and pressure-gradients all vary with time, so do the flows; we are everywhere dealing with unsteady motion of the blood. As we shall see, this greatly complicates the physical theory we have to use. Furthermore, it means that we need accurate measurements of instantaneous flow-rate or velocity, and very often simultaneous records of pressure, in order to understand events. Such records still represent a very considerable technical achievement, even in experimental animals where surgical access to large vessels is possible. In normal man, access to the systemic circulation is very limited, and we have inadequate information. It is only the increasingly thorough investigation of suspected cardio-vascular disease (particularly coronary artery disease) by catheter techniques that is slowly yielding a store of information about normal function.
In Fig. 12.16,
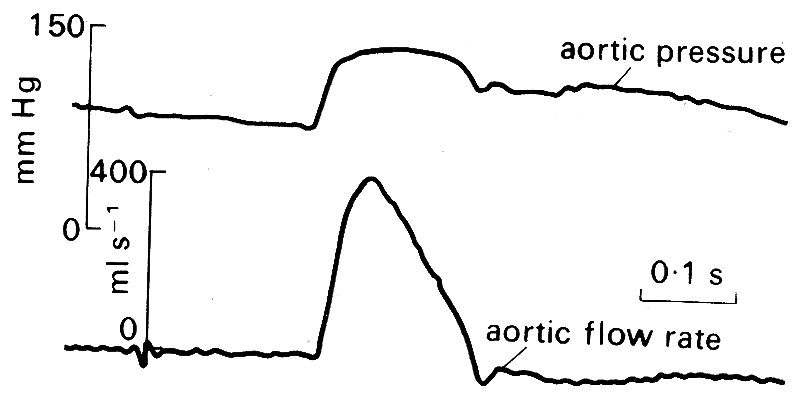
Fig. 12.16. Simultaneously records of pressure and flow-rate in the ascending aorta of a resting conscious dog. (After Noble (1968). "The contribution of blood momentum to left ventricular ejection in the dog'. Circulation Res. 23, 663-70.)
the pressure and flow velocity waveforms in the ascending aorta close to the aortic valve are shown. At resting heart-rates, the period of forward flow occupies about a quarter to a third of the cardiac cycle. When the heart-rate increases, for example in exercise, both systole and diastole shorten, but at different rates, diastole shortening to a much greater extent. Thus forward flow comes to occupy a greater proportion—up to 50 per cent—of the cycle at high heart-rates.
Forward motion of blood in the ascending aorta begins, of course, when the aortic valve opens and blood is ejected from the ventricle. The velocity rises rapidly to a peak, and promptly, but more slowly, falls again; there is a brief period of backward flow towards the aortic valve as it closes, and then the blood comes almost to rest for the remainder of the cardiac cycle. The maximum velocity observed depends on a large number of factors (not least the conditions of the experiment, such as the type and depth of anaesthesia) but in the normal conscious dog is probably in excess of 1 m s-1. (The values quoted in Table I are drawn from many sources in the literature and their wide range reflects the many influences which can act.) Acceleration at the beginning of ejection is abrupt and short-lived - the analogy has been drawn of the column of blood being struck by a hammer, and this is not entirely inappropriate, as can be seen from Fig. 12.17,
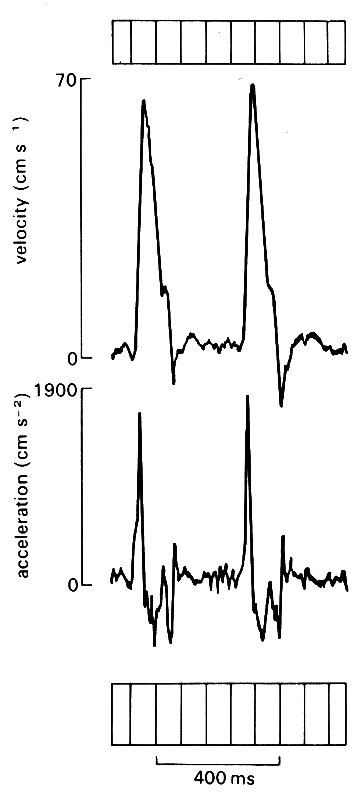
Fig. 12.17. Records of velocity (upper trace) and acceleration of blood flow in the ascending aorta in normal man. The acceleration record is obtained by electronic differentiation of the velocity signal. (From Bennett, Else, Miller, Sutton, Miller, and Noble (1974). 'Maximum acceleration of blood from the left ventricle of patients with ischaemic heart disease', Clin. Sci. mol. med. 46, 49-59.)
where the accelerations and decelerations which the blood undergoes are shown synchronously with the velocity waveform.* [*Acceleration is the rate of change of velocity, and is thus given by the slope of the velocity waveform. In mathematical notation it is the differential with respect to time, du/dt of the velocity u. In experimental work, acceleration is frequently derived from velocity signals by means of electronic differentiating circuits which give a voltage output proportional to the rate of change of their input signal. The same means can be used to derive rate of change of pressure from a pressure signal.]The peak acceleration is in the region of 5-10 g in the normal dog, and may increase up to 50 per cent when the heart is stimulated in exercise or by drugs. Values of velocity and acceleration are not yet well established in man, but are probably somewhat lower (Fig. 12.17).
The time-relationships between pressure and flow at the entrance to the aorta are illustrated in Fig. 12.18,
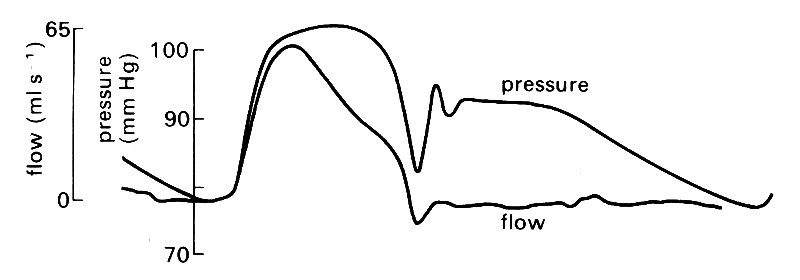
Fig. 12.18. Tracings of experimental pressure and flow records in the ascending aorta of the dog. The flow curve is scaled so that the peak height is comparable to the peak systolic pressure. (After Kouchoukos, Sheppard, and McDonald (1970). 'Estimation of stroke volume in the dog by a pulse contour method'. Circulation Res. 26, 611-23.)
where the wave-forms have been scaled to be of comparable size and superimposed. In early systole, pressure and flow-rate rise in phase with each other, a fact which serves to emphasize that it is the pressure gradient and not the pressure which drives the flow. Later in systole, the synchrony between pressure and flow-rate breaks down, chiefly due to the arrival of reflected components of the pressure wave; this subject will be examined later.
If we examine the velocity wave-form at points progressively further from the heart (Fig. 12.19, lower records)
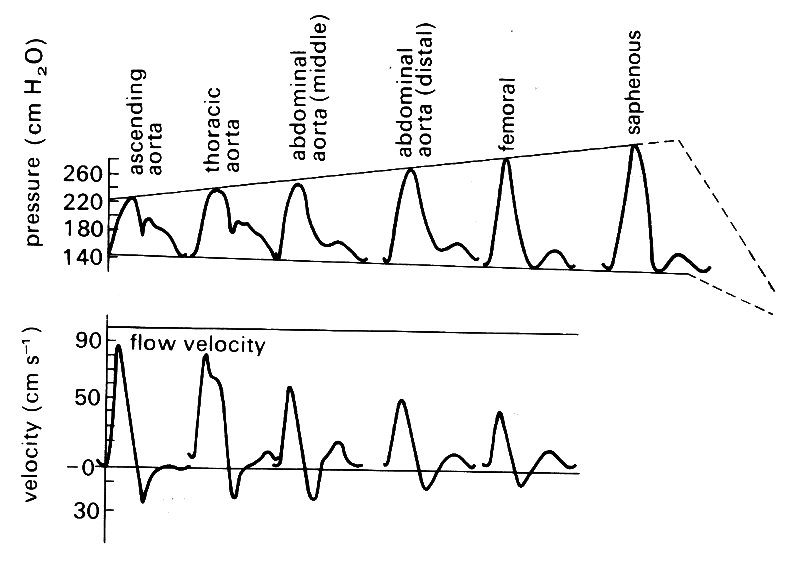
Fig. 12.19. Matched records of pressure and flow velocity at different sites in dog arteries. (After McDonald (1974). Blood flow in arteries. Edward Arnold, London.)
we see that the amplitude of the velocity wave-form decreases progressively; this is in contrast with the peaking and steepening of the pressure wave which we noticed earlier (Fig. 12.19, upper records). Later in this chapter (§12.3), we attempt to explain how these effects, and the others we have described, are brought about.
We find that if the detailed properties of the vascular bed are given, the pressure and flow pulses everywhere can in principle be predicted from either the pressure or the flow pulse at the root of the aorta. In particular, the pressure at the root of the aorta determines the flow there, and vice versa. Furthermore, although we do not have a complete description of the geometry and mechanical properties of blood vessels, there is enough information to permit the relationship between pressure and flow-rate throughout the aorta to be predicted with some accuracy.
12.2.4 Terminology. The unsteadiness of the flow and the presence of the velocity profile across an artery demand that we carefully define what we mean when we quote a velocity. If at any instant there is a volume flow-rate 0 throughout an artery of cross-sectional area A, then at that instant the cross-sectional average velocity is given by Q/A. This will vary with time, just as the flow-rate does, having an identical wave-form to it, merely scaled by a factor I/A. It is this instantaneous average velocity which is illustrated in most of the figures showing velocity wave-forms in this chapter.
However, the velocity within the vessel at that instant is not uniform across the cross-section, for example because of the presence of a boundary layer. In the case of Poiseuille flow (§5.1), it ranges from zero at the wall to twice the cross-sectional average at the centre-line. In large arteries, for reasons we shall be discussing later in this chapter, velocity profiles are very blunt (see, for example, Fig. 12.39) with narrow boundary layers close to the wall, and fluid outside the boundary layer (the 'core flow') travelling at a uniform velocity which is only slightly greater than the cross-sectional mean. Thus in large arteries it will be a good approximation (probably within 10 per cent) to equate velocity in the core (e.g. centre-line velocity) to cross-sectional average velocity.
Having seen that we can average the flow velocity spatially to give a cross-sectional average, we must now point out that we can also average the (unsteady) flow velocity with respect to time. Thus we can describe a mean or time-mean flow velocity, either for a particular point in the flow or for the whole flow. In Fig. 12.38, for example, the time-mean velocities at a whole series of points across each cross-section of the vessel are plotted, to give the time-mean or mean velocity profile.
Finally, we may in certain circumstances have to use a special form of averaging, known as ensemble averaging, to separate random velocity fluctuations such as turbulence which are superimposed upon the instantaneous velocity waveform. This is described, in its context, in §12.8.3.
12.2.5 Fourier analysis. This technique has proved so useful in the exploration and understanding of pressure and flow behaviour in large arteries that it is worth very briefly revising and expanding what was said about it in the earlier chapter on oscillations and wave-motion (§8.6). As was shown there, the analysis of an oscillatory wave is very simple if it has a sinusoidal form. Unfortunately, as many of the figures in this chapter show, pressure and flow waves in large arteries are not sinusoidal but have complicated shapes.
The basic principle of Fourier analysis is that any complicated periodic wave-form, like an arterial pressure wave, can be broken down into a set of sine waves, and resynthesized from them. These sine waves (which are called harmonics) will each have different amplitudes and different frequencies, and will be out of phase with each other. The process is useful because it is relatively simple to perform mathematical calculations with individual sine waves, while the composite wave is very unwieldy. For example, from a single sine wave of pressure, one can calculate the corresponding sine wave of flow-rate in an artery, on the basis of the simple theory outlined below (§12.3.5). Then the composite flow-rate wave-form can be constructed by adding together all the different flow-rate sine waves, with their different frequencies, amplitudes and phases. This can then be compared with observation. Equally, the pressure or flow-rate wave-form at one position in the artery can in principle be calculated from a knowledge of the pressure wave-form at a different position, as long as we also know the geometry and elastic properties of the arteries in between so that the way each component propagates can be calculated. (The gap between principle and practice is largely due to our incomplete knowledge of these properties.) The main limitation on such applications of Fourier analysis is that they are valid only if the system under study is linear, because otherwise the different harmonics do affect each other, and the behaviour of the composite wave cannot be predicted by superimposing separate sine waves. This is a very important restriction, discussed in detail in &12.3.4. As we shall see, linearity is a good approximation for arteries under physiological conditions.
The actual process of Fourier analysis is extremely laborious if performed by hand, and nowadays is normally done with the aid of a computer. The frequencies of the harmonics into which the wave is to be analysed are dictated by the repetition frequency of the wave itself (the fundamental frequency), and the first harmonic has this frequency. The second and subsequent harmonics have frequencies which are multiples of this frequency; thus if the fundamental frequency is 2 Hz, the second harmonic will be at 4 Hz, the third at 6 Hz, and so on. In general, the amplitude of successively higher harmonics falls steadily, until ultimately they can be ignored.
The practical test of the adequacy of a Fourier series in this respect is to put all the harmonics together again, and compare this result with the original wave-form. This is done repeatedly, adding successively higher harmonics until a satisfactory match is obtained. If the original waveform (e.g. blood pressure) oscillates about some non-zero mean level, this level will of course have to be included in the Fourier series as a constant term.
Aortic pressure and flow-rate wave-forms can be very accurately described by a constant term plus about 10 harmonics.* [*This means frequencies up to about 20 Hz in the dog, and 10 Hz in man. Measurement and recording systems must therefore have known properties up to these frequencies.] The amplitude of the harmonics up to the tenth is shown in Fig. 12.20.
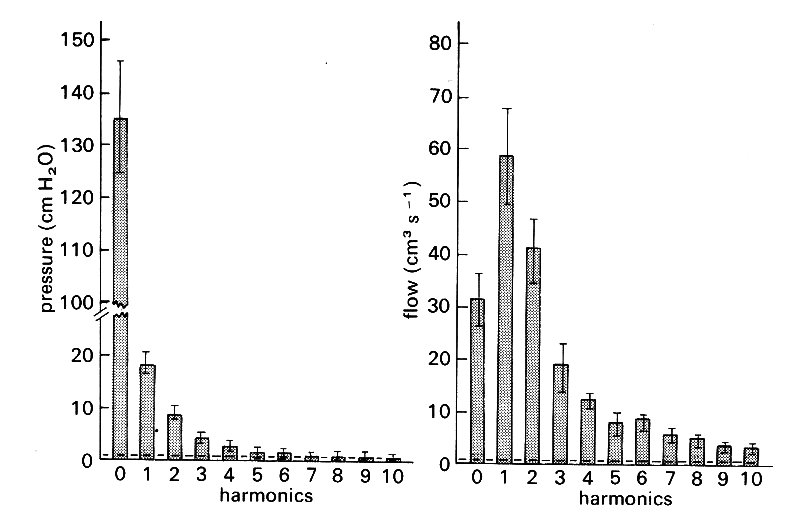
Fig. 12.20. Harmonic content of the pressure and flow curves measured at the root of the aorta. Averaged results from eight dogs. The bars about the mean values represent the standard error of the mean. The horizontal lines near zero are the noise levels of'the recording equipment. (After Patel, de Freitas, and Fry (1963). 'Hydraulic input impedance to aorta and pulmonary artery in dogs'. J. Appl. Physiol. 18, 134-40.)
Predictably, in the case of the pressure, the constant term is the largest; very small higher frequency terms are chiefly necessary to describe the sharp fluctuations of the dicrotic notch. In the case of flow-rate, the constant term is relatively much smaller, and the fundamental much larger. The higher frequencies here are necessary to describe the very rapid rise in flow in early systole, and the sharp fluctuations when flow reversal occurs at the end of systole. The accuracy with which a constant term and ten harmonics describes the original wave-form is demonstrated by resynthesis in Fig. 12.21.
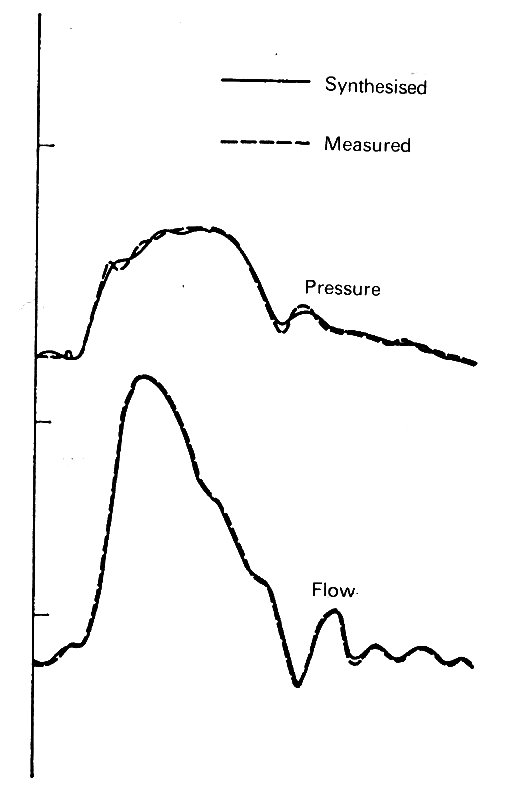
Fig. 12.21. Pressure and flow wave-forms in the ascending aorta, as measured and as resynthesized from the constant term and the first ten harmonics of a Fourier analysis. These obviously describe the waves very adequately. (From McDonald (1974). Blood flow in arteries. Edward Arnold, London.)
Further from the heart, where the wave-forms are smoother, they may be adequately described by fewer harmonics. In §8.6, for example we showed how the flow-rate wave-form may be approximately reconstructed from four harmonics.
Finally, a note of warning should be sounded; one cannot get more out of a Fourier series than is put in. In other words, if the original wave-form is faulty for some reason (e.g. instrumental inadequacy) then so will be the Fourier series describing it. Suppose, for example, that we record arterial pressure with a transducer which has a limited frequency response and can only 'follow' up to the frequency of the fifth harmonic. Then if we perform a Fourier analysis on the recorded signal, we shall get the impression that no harmonics above the fifth are of significant amplitude. The inverse of this occurs if we know, from testing, that the pressure transducer can faithfully pick up frequencies going higher than that of the fifth harmonic. Then if our Fourier analysis shows only five harmonics of significant amplitude, we can be sure that we are not misled about the shape of the recorded wave. In fact, this actually gives us a method of checking the validity of recorded wave-forms, and has been one of the most useful applications of Fourier analysis in the past. Another related use has been in the correction of the recorded wave-form; if we have a pressure transducer which distorts certain frequencies in a known way - a common problem - we can do a Fourier analysis on the recorded wave-form, correct the amplitude and phase of harmonics whose frequencies fall in the distorted region, and then resynthesize a corrected wave-form. Thus Fourier analysis is an extremely useful practical tool as well as a framework for the understanding of pressure and flow behaviour in arteries.